Как вписать окружность в равнобедренную трапецию пошаговая инструкция - Arganabio.ru - инструкции по эксплуатации и многое другое

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

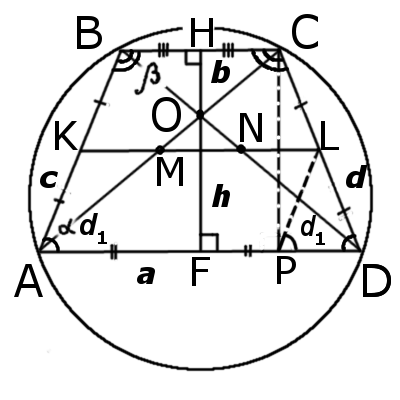
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

Как вписать окружность в трапецию равнобедренную

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Рис.1

Признаки равнобедренной трапеции

∠ABC = ∠BCD и ∠BAD = ∠ADC

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

Основные свойства равнобедренной трапеции

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

a = b + 2 h ctg α = b + 2 c cos α

b = a — 2 h ctg α = a — 2 c cos α

c =	h	=	a — b
sin α	2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d ₁ 2 — c 2	b =	d ₁ 2 — c 2	c = √ d ₁ 2 — ab
b	a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b b =	2S	— a
h	h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

m = a — h ctg α = b + h ctg α = a — √ c 2 — h 2 = b + √ c 2 — h 2

2. Формула средней линии трапеции через площадь и сторону:

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√ 4 c 2 — ( a — b ) 2
2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
2

Диагонали равнобедренной трапеции

Формулы длины диагоналей равнобедренной трапеции:

d ₁ = √ a 2 + c 2 — 2 ac cos α

d ₁ = √ b 2 + c 2 — 2 bc cos β

4. Формула длины диагонали через высоту и основания:

d ₁ =	1	√ 4 h 2 + ( a + b ) 2
2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√ 4 c 2 — ( a — b ) 2
4

2. Формула площади через стороны и угол:

S = ( b + c cos α ) c sin α = ( a — c cos α ) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
sin α	sin β

4. Формула площади через основания и угол между основой и боковой стороной:

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = ( a + b ) · r = √ ab ·c = √ ab ·m

6. Формула площади через диагонали и угол между ними:

S =	d ₁ 2	· sin γ	=	d ₁ 2	· sin δ
2	2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d ₁
4√ p ( p — a )( p — c )( p — d ₁)

a — большее основание

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

Если MN —

По свойству равнобедренной трапеции,

Из прямоугольного треугольника ABF по теореме Пифагора

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

Трапеция. Свойства трапеции

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

источники:

http://b4.cooksy.ru/articles/kak-vpisat-okruzhnost-v-trapetsiyu-ravnobedrennuyu

Трапеция. Свойства трапеции

Источник

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

$[AB = CD = frac{{AD + BC}}{2}.]$

Если MN —

средняя линия

трапеции ABCD,

AD||BC, то

$[MN = AB = CD = frac{{AD + BC}}{2}.]$

По свойству равнобедренной трапеции,

$[AF = DK = frac{{AD - BC}}{2}.]$

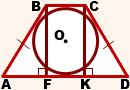
Если AD=a, BC=b,

$[AF = DK = frac{{a - b}}{2}.]$

$[AB = frac{{a + b}}{2}.]$

Из прямоугольного треугольника ABF по теореме Пифагора

$[B{F^2} = A{B^2} - A{F^2},]$

$[B{F^2} = {(frac{{a + b}}{2})^2} - {(frac{{a - b}}{2})^2}]$

$[B{F^2} = frac{{{{(a + b)}^2} - {{(a - b)}^2}}}{4}]$

$[B{F^2} = frac{{(a + b - a + b)(a + b + a - b)}}{4}]$

$[B{F^2} = frac{{2b cdot 2a}}{4} = ab,]$

$[r = frac{1}{2}sqrt {ab} .]$

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

AK=AP=DP=DN,

BK=BF=CF=CN.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

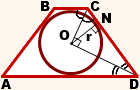
Значит, треугольник COD — прямоугольный,

(как радиус, проведенный в точку касания).

Следовательно, ON — высота, проведённая к гипотенузе,

Источник

Окружность, вписанная в трапецию

Что такое окружность, вписанная в трапецию

Окружность можно вписать в любой треугольник. Однако это утверждение нельзя применить к любому из четырехугольников.

Прежде чем приступить к рассмотрению темы о вписанной в трапецию окружности, дадим определение вписанной окружности.

Вписанной в многоугольник окружностью называют окружность, которая касается каждой из сторон многоугольника в одной точке. Многоугольник в этом случае называют описанным около окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Теорема 1

Теорема о вписанной окружности: в произвольный выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Доказательство: пусть имеется произвольный четырехугольник MNKL и вписанная в него окружность. Обозначим точки касания окружности со сторонами четырехугольника как O, P, R, S.

Если касательные проведены из одной точки, то отрезки, построенные от этой точки до точки касания с окружностью, равны. Тогда KS=KR, LS=LO, MO=MP, NR=NP. Вычислим суммы противоположных сторон: MN+KL=(MP+NP)+(KS+LS) и NK+ML=(NR+KR)+(MO+LO).

Из равенства отрезков получим, что MN+KL= NK+ML.

Примечание 1

Четырехугольник считают выпуклым, если он расположен в одной полуплоскости относительно линии, проходящей через любую из его сторон.

Трапеция является выпуклым четырехугольником. При этом две параллельные стороны трапеции называют основаниями, а две остальные — боковыми сторонами.

Тогда необходимым условием наличия вписанной окружности в трапецию будет равенство суммы ее оснований и боковых сторон.

Для обратного случая — окружность описана вокруг трапеции, трапеция должна быть равнобедренной, то есть ее боковые стороны должны быть равными.

Рассмотрим свойства вписанной в трапецию окружности.

Из свойства биссектрис при боковых сторонах трапеции следует, что радиусы вписанной окружности, проведенные к вершинам боковой стороны и лежащие на биссектрисах, образуют прямой угол.

Примечание 2

Биссектрисы трапеции пересекаются под углом 90°.

Радиус вписанной окружности, проведенный к точкам касания, перпендикулярен сторонам трапеции (по свойству перпендикулярности радиуса и касательной).

Из предыдущего свойства вытекает следующее: радиус вписанной окружности равен половине высоты трапеции, а диаметр — полной длине высоты.

Примечание 3

Высота трапеции — прямая, опущенная от одного основания к другому под прямым углом.

Где находится центр такой окружности

Для построения и решения задача необходимо определить, где расположен центр вписанной окружности.

Примечание 4

Центр окружности, вписанной в трапецию, лежит в точке пересечения биссектрис.

Биссектрисы трапеции пересекаются под прямым углом, отсюда можно сделать следующий вывод: треугольники MON и KOL — прямоугольные.

Формулы для расчета

Основными характеристиками любой окружности являются радиус и диаметр.

Точка касания окружности радиусом R и боковой стороны делит последнюю на два отрезка v и q. Тогда формула для вычисления радиуса будет иметь вид:

Формула 1

(R=sqrt{vcdot q})

Если трапеция равнобедренная и сумма длин оснований равна двум длинам боковой стороны, радиус вписанной окружности:

Формула 2

(R=frac{sqrt{vcdot q}}2)

Диаметр равен длине двух радиусов, значит:

Формула 3

(D=2sqrt{vcdot q})

Формула радиуса через высоту трапеции:

Диаметр через высоту:

Если значение высоты неизвестно, ее можно найти через длины диагоналей (d_1) и (d_2) и оснований a и b трапеции:

Формула 6

(h=frac{d_1cdot d_2}{a+b}singamma)

где γ — угол между диагоналями трапеции.

Площадь вписанной окружности через параметры трапеции (высоту, отрезки боковой стороны):

Формула 7

(S=pi R^2=frac14pi h^2)

или

Формула 8

(S=pi R^2=picdot vcdot q)

В случае равнобедренной трапеции:

Формула 9

(S=pi R^2=frac{picdot vcdot q}4)

Периметр вписанной окружности через параметры трапеции:

Формула 10

(P=2mathrm{πR}=mathrm{πh})

или

Формула 11

Если трапеция равнобедренная:

Формула 12

(P=2mathrm{πR}=mathrmpisqrt{mathrm{vq}})

Приведем формулы для вычисления произвольной и равнобедренной трапеции через радиус вписанной окружности R.

Площадь трапеции:

Формула 13

(S=frac{a+b}2h=(a+b)R)

Полусумма оснований a и b равна средней линии l, тогда:

Формула 14

(S=2cdot lcdot R)

Площадь равнобедренной трапеции:

Формула 15

( S=frac{4R^2}{sinalpha})

где α — угол между основанием и боковой стороной.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

25
Июл 2013

Категория: Справочные материалы

Трапеция. Свойства трапеции

2013-07-25
2016-06-15

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия – $k=frac{AD}{BC}.$

Отношение площадей этих треугольников есть .

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Площадь

$S=frac{a+b}{2}cdot h$ или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Смотрите также площадь трапеции.

Автор: egeMax |

комментарий 431

Печать страницы

Источник

Вписанная в равнобедренную трапецию окружность указывает на некоторые особенности данной трапеции.
Рассмотрим их.

Окружность в трапецию можно вписать только в том случае, когда суммы попарно противоположных сторон одинаковые.

Другими словами, окружность в трапецию можно вписать тогда, когда:
AB + CD = AD + BC.
Справедливым будет и обратное утверждение:
Если суммы попарно противоположных сторон трапеции одинаковые, то в такую трапецию можно вписать окружность.
Из всего вышесказанного следует, что если трапеция равнобедренная, то:

$[bok.storona1=bok.storona2=frac{osnovanie1+osnovanie2}{2}.]$

По свойству средней линии, если в равнобедренную трапецию можно вписать окружность, то ее боковые стороны длине средней линии.

$[sredn.liniya=bok.storona1=bok.storona2=frac{osnovanie1+osnovanie2}{2}]$

Высоту равнобедренной трапеции можно выразить через основания этой трапеции.

Согласно одному из свойств равнобедренной трапеции запишем:

$[AF=KD=frac{osnovanie1-osnovanie2}{2}.]$

Боковая сторона такой трапеции равна:

$[bok.storona1=bok.storona2=frac{osnovanie1+osnovanie2}{2}.]$

Рассмотрим прямоугольный треугольник ABF.
По теореме Пифагора запишем:

$[{BF}^2={AB}^2-{AF}^2;]$

$[{BF}^2={left(frac{osnovanie1+osnovanie2}{2}right)}^2-{left(frac{osnovanie1-osnovanie2}{2}right)}^2;]$

$[{BF}^2=frac{{left(osnovanie1+osnovanie2right)}^2-{left(osnovanie1-osnovanie2right)}^2}{4}.]$

Источник

Рассмотрим частный случай вписанной в трапецию окружности.

Если в равнобедренную трапецию вписана окружность, существует несколько направлений, по которым можно повести решение задачи.

1. В равнобедренную трапецию вписана окружность, которая в точке касания делит боковую сторону на отрезки m и n. Найти площадь трапеции.

Решение:

1)∠ADC+∠BCD=180º(как внутренние односторонние при AD∥BC и секущей CD).

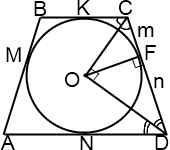
2) Так как центр вписанной окружности — точка пересечения биссектрис трапеции, то

∠OCD+∠ODC=90º.

3) Так как сумма углов треугольника равна 180º, в треугольнике OCD ∠COD=90º.

4) OF перпендикулярен CD (как радиус, проведенный в точку касания), следовательно, в треугольнике OCD OF — высота, проведенная к гипотенузе. По свойству прямоугольного треугольника,

Так как высота трапеции равна диаметру вписанной окружности, то

5) Формула для нахождения площади трапеции

$[S = frac{{a + b}}{2} cdot h]$

Так как в трапецию вписана окружность, суммы ее противолежащих сторон равны:

Таким образом, площадь трапеции равна

$[S = frac{{2(m + n)}}{2} cdot 2sqrt {mn} = 2(m + n)sqrt {mn} .]$

2. В равнобедренную трапецию вписана окружность, которая в точке касания делит боковую сторону на отрезки m и n.Найти периметр трапеции.

Решение:

CD=CF+FD=m+n.

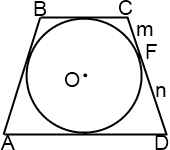
AB=CD (по условию).

AD+BC=AB+CD (так как в трапецию вписана окружность).

P=AD+BC+AB+CD=4(m+n).

3.В равнобедренную трапецию вписана окружность. Найти высоту трапеции, если известны ее основания: AD=a, BC=b.

Решение:

Проведем высоты трапеции BP и CE. Четырехугольник BCEP- прямоугольник (так как у него все углы прямые). Следовательно, PE=BC=b.

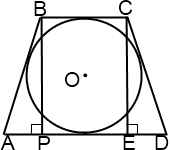
Прямоугольные треугольники треугольники ABP и DCE равны по катету и гипотенузе. Отсюда,

$[AP = DE = frac{{AD - BC}}{2} = frac{{a - b}}{2}.]$

Поскольку в трапецию вписана окружность, AB+CD=AD+BC=a+b,

$[AB = frac{{AB + CD}}{2} = frac{{a + b}}{2}.]$

Из треугольника ABPпо теореме Пифагора

$[B{P^2} = A{B^2} - A{P^2}]$

$[B{P^2} = {(frac{{a + b}}{2})^2} - {(frac{{a - b}}{2})^2} = ]$

$[begin{array}{l} = (frac{{a + b}}{2} - frac{{a - b}}{2})(frac{{a + b}}{2} + frac{{a - b}}{2}) = ab.\A{B^2} - A{P^2}end{array}]$

Таким образом,

Вывод:

Если в равнобедренную трапецию вписана окружность, высота трапеции есть среднее пропорциональное между ее основаниями.

Источник

Трапеция и ее свойства

Т. А. Унегова

Определения:

Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция называется равнобедренной.

Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.

Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.

Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теоремы о средней линии и диагоналях трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: $m=displaystyle frac{a+b}{2}$ .

Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: $EF=GH, ; FG=displaystyle frac{a-b}{2}$ .

Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: PQ=MN .

Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.

Эта теорема называется также «Замечательное свойство трапеции».

Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.

Теоремы о площади трапеции

Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: $S=displaystyle frac{a+b}{2}cdot h$ .

Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: S=mh .

Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: $S=displaystyle frac{1}{2}d_1d_2{sin alpha }$ , где d_1=AC, d_2=BD, (Вместо можно брать

Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: S=pr . Таким образом, $S=displaystyle frac{a+b+c+d}{2}cdot r$ .

Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)

Теоремы о вписанных и описанных трапециях

Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.

Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Задача 1.

Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны sqrt{2} .

Решение:

Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна sqrt{2} , то по теореме Пифагора получаем, что h=2 .

Ответ: 2.

Задача 2.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ${150}^{{}^circ }$ . Найдите площадь трапеции.

Решение:

Углы angle ABC и angle BAH — односторонние, их сумма равна ${180}^{{}^circ }$ , и тогда angle BAH $=30{}^circ .$

Из ABH найдем высоту BH. Катет, лежащий против угла в ${30}^{{}^circ }$ , равен половине гипотенузы. Получаем, что BH = 3,5.

Площадь трапеции равна $S=displaystyle frac{6+18}{2}cdot 3,5=42$ .

Ответ: 42.

Задача 3.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.

Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что x=5.

Ответ: 5.

Задача 4.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.

Ответ: 0,5.

Задача 5.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

Периметр треугольника равен сумме его сторон, то есть

Периметр трапеции равен

Ответ: 23.

Задача 6.

В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол $63{}^circ$ . Найдите углы трапеции.

Решение:

Пусть angle CAD =alpha , тогда angle CAB =alpha и angle BAD =2alpha , так как трапеция равнобедренная.

Сумма углов $vartriangle ACD=3alpha +63{}^circ =180{}^circ$ , откуда
$alpha =39{}^circ .$
Итак, $angle D=78{}^circ$ , а $angle BCD=180{}^circ -78{}^circ =102{}^circ$ .

Ответ: $78{}^circ , 102{}^circ$ .

Задача 7.

В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и $h^2={25}^2-7^2=left(25-7right)left(25+7right)=18cdot 32.$ Отсюда,

Ответ: 24.

Задача 8.

Тупой угол равнобедренной трапеции равен ${135}^circ$ , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом $45{}^circ$ .

Каждый треугольник равнобедренный, поэтому h = 1,4.

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна $displaystyle frac{2+4,8}{2}cdot 1,4=4,76$ .

Ответ: 4,76.

Задача 9.

Площадь трапеции равна 60м ^2, а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции $S=displaystyle frac{a+b}{2}cdot h$ , то $60=displaystyle frac{8+12}{2}cdot h$ , откуда h = 6.

Ответ: 6.

Задача 10.

В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.

Решение:

Проведем CE BD и DE — продолжение AD.

Так как BCDE — параллелограмм, то CE = a.

По теореме 10 получим, что $S_{ABCD}=S_{ACE}=displaystyle frac{1}{2}a^2$ .

Ответ: $displaystyle frac{1}{2}a^2$

Задач 11.

В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.

Найдите AD, если периметр трапеции равен 20, а угол D равен $60{}^circ$ .

Решение:

По условию задачи в прямоугольном ACD

angle D $=60{}^circ$ , следовательно, angle CAD $=30{}^circ$ .

Так как AC — биссектриса, то angle CAB $=30{}^circ$ , откуда angle DAB $=60{}^circ$ , то есть, трапеция равнобедренная. angle BCA =angle CAD $=30{}^circ$ как накрест лежащие, поэтому ABC — равнобедренный.

Обозначим длины боковых сторон ABC буквой x.

Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в $30{}^circ$ лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда

x = 4 и AD = 8.

Ответ: 8.

Задача 12.

В равнобедренной трапеции ABCD с острым углом $60{}^circ$ меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?

Решение:

Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и BCM подобен ADM c коэффициентом .

Пусть $S_{BCM}$ =S_1 , $S_{ADM}=S_2$ , тогда

$S_2=k^2cdot S_1=36{cdot S}_1.$

Площадь трапеции будет равна

$S_{ABCD}=S_2-S_1=36 S_1-S_1=35 S_1=35 S_{BCM}.$

Ответ: 35.

Задача 13.

Сумма углов при одном из оснований трапеции равна $90{}^circ$ . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.

Так как сумма углов при основании трапеции равна $90{}^circ$ , то $angle BEC=90{}^circ$ , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит

Ответ: 2.

Задача 14.

Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна S=mh , а высота трапеции равна диаметру вписанной окружности, то есть h=2r, то , откуда r=1,2 .

Ответ: 1,2.

Задача 15.

Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

откуда

Сторона AB равна диаметру окружности, поэтому r=3 .

Ответ: 3.

Задача 16.

Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

$m=displaystyle frac{a+b}{2}=displaystyle frac{c+d}{2}=displaystyle frac{40}{2}=20.$

Ответ: 20.

Задача 17.

В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как AD — диаметр окружности, то дуга ABCD равна $180{}^circ$ . Она делится на три равные части по $60{}^circ .$

Вписанный угол D опирается на дугу ABC, которая равна $120{}^circ$ , отсюда $angle ADC=60{}^circ$ и, стало быть, $angle C=120{}^circ =angle B.$

Ответ: 120.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.04.2023

Источник