Какое свойство алгоритма определяет однозначность исполнения инструкций

Свойства алгоритма

При составлении
и записи алгоритма необходимо обеспечить,
чтобы он обладал рядом свойств. Рассмотрим
эти свойства на следующем примере: пусть
требуется вычислить сумму двух целых
чисел и вывести на экран результат.

Однозначность
алгоритма,
под которой понимается единственность
толкования исполнителем правил выполнения
действий и порядка их выполнения. Чтобы
алгоритм обладал этим свойством, он
должен быть записан командами из системы
команд исполнителя.

Для нашего примера
исполнитель алгоритма должен понимать
такую запись действий, как сложить числа
А и В.

Конечность
алгоритма
— обязательность
завершения каждого из действий,
составляющих алгоритм, и завершение
выполнения алгоритма в целом, т.е.
алгоритм должен заканчиваться после
конечного числа шагов.

Результативность
алгоритма,
предполагающая, что выполнение алгоритма
должно завершиться получением определенных
результатов. Алгоритм в нашем примере
обладает этим свойством, так как для
целых чисел А и В всегда будет вычислена
сумма.

Массовость,
т. е. возможность применения данного
алгоритма для решения целого класса
задач, отвечающих общей постановке
задачи. Для того чтобы алгоритм обладал
свойством массовости, следует составлять
алгоритм, используя обозначения величин
и избегая конкретных значений.

Правильность
алгоритма,
под которой понимается способность
алгоритма давать правильные результаты
решения поставленных задач. Представленный
в примере алгоритм обладает свойством
правильности, так как в нем использована
правильная формула сложения целых
чисел, и для любой пары целых чисел
результат выполнения алгоритма будет
равен их сумме.

Определенность
алгоритма.
Каждый шаг алгоритма должен быть
определен.

Входные данные
алгоритма.
Алгоритм
должен иметь некоторое (может быть
равное 0) число входных данных.

Выходные данные
алгоритма.
Результатом выполнения алгоритма должна
быть одна или несколько выходных величин,
зависящих от исходных данных.

Эффективность
алгоритма.
Алгоритм должен быть эффективным, т.е.
результат должен быть получен наименьшим
числом наиболее простых операций.

Типы вычислительных процессов

Вычислительные
процессы могут быть: линейные,
разветвляющиеся и циклические.

Линейные алгоритмы
— это алгоритм,
в котором все его действия выполняются
одно за другим, т.е. последовательно.

Однако в большинстве
вычислительных процессов мы сталкиваемся
с тем, что выбор хода дальнейших действий
определяется результатом предыдущих.
Такие алгоритмы называются разветвляющимися.

Разветвляющиеся
алгоритмы
— это алгоритмы, в которых в зависимости
от выполнения или не выполнения некоторого
условия совершается одна или другая
последовательность действий.

Циклические
алгоритмы—
алгоритмы, в которых одна и та же
последовательность действий совершается
несколько раз до тех пор, пока выполняются
некоторые условия.
На рисунке представлено графическое
представление вычислительных процессов

Рисунок 2 Типы
вычислительных процессов

Блок-схемы алгоритмов

Блок схема
– это графическое представление
алгоритма при помощи стандартных
обозначений. Блок схемы составляются
в соответствии с ГОСТами. ГОСТы алгоритмов:
ГОСТ 19.002-80, ГОСТ 19.003-80. На схемах алгоритмов
выполняемые действия изображаются в
виде отдельных блоков, которые соединяются
между собой линиями связи в порядке
выполнения действий. На линиях связи
могут ставиться стрелки, причем, если
направление связи слева
направо или сверху вниз,
то стрелки не
ставятся.
Блоки нумеруются. Внутри блока дается
информация о выполняемых действиях.

Таблица
1 – Основные блоки, используемые при
составлении алгоритмов

Название	Обозначение	Назначение
Пуск, Останов		Начало-конец алгоритма
Процесс		Любое вычислительное действие
Решение		Проверка условия
Модификатор		Цикл
Ввод-вывод		Ввод-вывод данных
Документ		Вывод на печатающее устройство
Соединитель		Используется на линиях разрыва
Комментарий		Комментарий

Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки

Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании

---

---

Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.

■  Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.

Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.

Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.

Свойства алгоритмов

Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:

• Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
• Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
• Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
• Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
• Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.

Способы представления алгоритмов:

• словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
• блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
• формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
• псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.

Словесная запись алгоритма

Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.

■  Пример 1. Записать в словесной форме правило деления обыкновенных дробей.

Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.

Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).

Формальные исполнители алгоритма

Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.

Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).

Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.

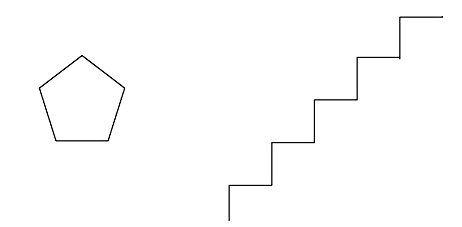
■ Пример 2. Исполнитель Крот имеет следующую систему команд:

1. вперед k — продвижение на указанное число шагов вперед;
2. поворот s — поворот на s градусов по часовой стрелке;
3. повторить m [команда1 … командаN] — повторить m раз серию указанных команд.

Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?

Повторить 5 [вперед 10 поворот 72]

Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.

Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).

■ Пример 3.  В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).

Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).

Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]

Блок–схема

Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).

Основные элементы блок–схемы алгоритма:

Общий вид блок–схемы алгоритма:

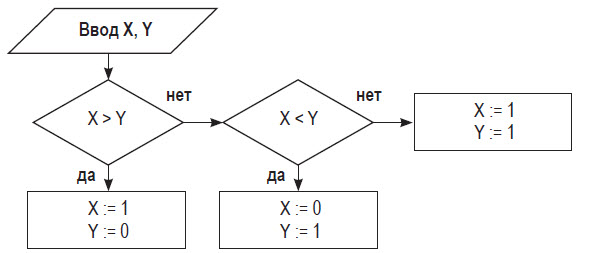
■ Пример 4.  Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.

Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.

Решение.

1. Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
2. В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
3. Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
4. Вычисляется результат выполнения алгоритма: X := 0, Y := 1.

Ответ: X := 0, Y := 1.

Алгоритмические языки

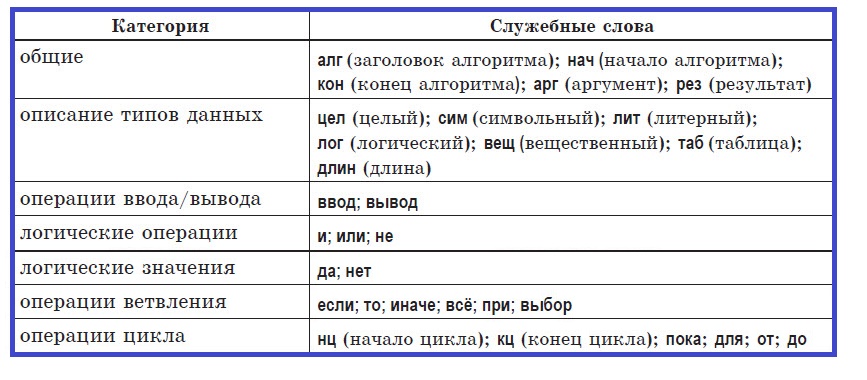
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.

В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.

Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.

Псевдокод

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.

Служебные слова учебного алгоритмического языка:

Стандартная структура алгоритма

Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.

Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.

В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.

Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.

Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.

Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.

Описание величин и действия над ними

При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.

При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.

Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.

В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.

При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.

Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).

Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.

Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.

Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10^-2 и –7,123456*10²).

Над числовыми данными можно выполнять арифметические операции и операции сравнения.

Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.

Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.

Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».

Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.

Команды учебного алгоритмического языка

Учебный алгоритмический язык использует следующие команды для реализации алгоритма:

ОПЕРАЦИЯ ПРИСВАИВАНИЯ

Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.

Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).

Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.

ВВОД И ВЫВОД ДАННЫХ

В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.

При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.

Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.

В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.

Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.

Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).

Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:

Путь 200 м

Тот же результат был бы получен, если бы изменить строку вывода на

вывод «Путь «, v * t, » м»

---

Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки».

Вернуться к Списку конспектов по информатике.

Статья расскажет о происхождении термина «Алгоритм» и о том, какими свойствами он обладает.

Алгоритмом называют определенную конечную последовательность действий (набор инструкций), выполнение которых приводит к достижению конкретной цели (решению поставленной задачи). В литературе по информатике, как и на просторах глобальной сети, можно найти множество общей теоретической информации относительно понятия и решения алгоритма. Достаточно запомнить основную мысль: достижение алгоритмического результата обеспечивается выполнением определенной последовательности действий (чаще всего, действий арифметических или логических).

История возникновения термина

Сегодня это понятие является фундаментальным и в математике, и в информатике. Однако сам термин возник задолго до появления компьютеров и прочих электронных средств вычислительной техники. Впервые об алгоритме заговорили в средние века — именно тогда европейские ученые ознакомились с методами вычисления арифметических действий, производимых в десятичной системе счисления азиатским математиком по имени Мухаммед ибн Муса аль-Хорезми (от имени этого математика и сформировался термин Algorithm). Сочинение аль-Хорезми перевели, а в последующие столетия появилось много трудов, посвященных вопросу обучения искусству счёта посредством цифр. Можно вспомнить описание алгоритма в европейской науке в те годы:

Также значение слова «алгоритм» сегодня нередко связывают со значениями таких слов, как «рецепт», «метод», «процесс», «инструкция».

Исполнитель и программа

Судя по историческим справкам, изначально речь шла о способе выполнения арифметических действий над десятичными числами. Прошли годы. Понятие стали применять при обозначении любой последовательности действий, которая приводит к получению требуемого результата. Причем алгоритмы существуют не сами по себе — они предназначаются для конкретного исполнителя. Кто может выступать таким исполнителем:
— человек;
— роботизированное/автоматизированное устройство, механизм;
— компьютер;
— язык программирования и т. д.

Отличительная черта исполнителя — способность выполнять команды, которые включены в алгоритм. Это становится возможным, благодаря описанию последнего на формальном языке, который исключает неоднозначность толкования. Множество команд задано изначально строго и является конечным. Действия, которые должен выполнить исполнитель, называют элементарными действиями, а сама запись алгоритмической последовательности на формальном языке — это программа. Разработка алгоритма в целях решения задачи — это алгоритмизация.

Главные характеристики

Выделяют следующие свойства алгоритма: массовость, дискретность, результативность, определенность, понятность, формальность, завершаемость. Будет не лишним рассмотреть их более подробно, дав каждому свойству алгоритма пояснение:
1. Массовость (универсальность). Благодаря этому свойству, алгоритм можно успешно применять к различным наборам исходных данных. Пусть существует запись некой абстрактной последовательности, выраженная формулой. Подставляя в эту формулу значения (каждый раз новые), пользователь будет получать верные решения в соответствии с определенным алгоритмом действий.
2. Дискретность (разрывность). Это свойство характеризует структуру. Каждая алгоритмическая последовательность действий делится на этапы (шаги), а процесс решения задачи — это последовательное исполнение простых шагов. Также дискретность обозначает, что для выполнения каждого этапа потребуется конечный временной отрезок (исходные данные преобразуются во времени в результат дискретно).
3. Определенность (точность, детерминированность) — это свойство указывает алгоритму, что каждый его шаг должен быть строго определенным, то есть различные толкования должны быть исключены. Строго определяется и порядок выполнения шагов. В результате каждый шаг определяется состоянием системы однозначно, когда четко понятно, какая команда станет выполняться на следующем шаге. Как итог — при любом исполнителе для одних и тех же исходных данных при выполнении одной и той же цепочки команд будет выдаваться одинаковый результат. Да, существуют вероятностные алгоритмы — в них на последующий шаг влияют как текущее состояние системы, так и генерируемое случайное число. Но при включении способа генерации рандомных чисел в перечень «исходных данных», вероятностный алгоритм превращается в подвид обычного.
4. Понятность. Должны быть включены лишь те команды, которые доступны и понятны исполнителю, то есть входят в систему его команд.
5. Формальность. Любой исполнитель действует формально и лишь выполняет инструкции, не вникая в смысл. Он не отвлекается от поставленной задачи и не рассуждает, зачем и почему они нужны. Рассуждениями занимается разработчик алгоритма, задача же исполнителя — просто исполнить предложенные команды и получить результат. «Приказы не обсуждают, а выполняют».
6. Завершаемость (конечность). Если исходные данные заданы корректно, алгоритм завершит свое действие и выдаст результат за конечное число шагов.
7. Результативность. Согласно этому свойству, любой алгоритм должен завершаться конкретными результатами.

Основные виды алгоритмов

В информатике и программировании выделяют много видов алгоритмов. Основные из них:
— линейные (команды выполняются последовательно, одна за одной);
— разветвляющиеся (есть условие, при проверке которого возможно разветвление на несколько параллельных ветвей);
— циклические (предусматривается многократное повторение одних и тех же действий).

Источники:
• https://math-it.petrsu.ru/users/semenova/Informatika/DOC/Sam_Izuch/Algoritm.pdf;
• https://www.sites.google.com/site/algoritmyvidyisvojstva/materialy/materialy-1.

Результат участника

Название конкурса: Конкурс по информатике «Алгоритм и его свойства»
Участник: Алешин Дмитрий

Результат (баллов): 8 из 10

Затрачено времени: 2:34
Дата участия: 20.12.2021
Идентификатор результата: A487 314431

Ответы участника
Вопрос № 1. Понятность

Какое свойство алгоритма определяет, что инструкции алгоритма должны быть составлены только из команд, входящих в систему команд исполнителя?

Вопрос № 2. Понятность

Какое свойство алгоритма определяет однозначность исполнения инструкций?

Вопрос № 3. Дискретность

Какое свойство алгоритма определяет, что инструкции алгоритма должны быть отделены одна от другой?

Вопрос № 4. Детерминированность

Какое свойство алгоритма нарушается в рецепте приготовления кофе?
В 100 мл воды положить 2 ложки кофе и 1 ложку сахара. Тщательно перемешать. Добавить кардамон по вкусу.

Вопрос № 5. Блок «Конец»

Какой блок на языке блок-схем имеет одну входящую стрелку и не может содержать исходящую стрелку?

Вопрос № 6. Правильные конструкции языка программирования

Синтаксис языка программирования описывает …

Вопрос № 7. Условный

Алгоритм поиска максимума из двух заданных чисел a, b:
если a > b, то максимум = a, иначе максимум = b.
К какому виду относится этот алгоритм?

Вопрос № 8. Графическая

К какому способу записи алгоритма относится язык блок-схем?

Вопрос № 9. E, A, C, G, H

Составьте подходящую последовательность шагов для алгоритма похода в магазин за покупками.
A – зайти в банк
B – выйти из магазина
C – взять хлеб
D – зайти в магазин
E – выйти из дома
F – дойти до дома
G – взять молоко
H – оплатить покупки

Вопрос № 10. Время работы и объем используемой памяти

Какие характеристики сравнивают для оценки эффективности алгоритмов?

Нажмите правой кнопкой мышки на картинке и выберите «Сохранить изображение как…»

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Тема
  Алгоритмы
  Виды алгоритмов
  Свойства алгоритмов
  МБОУ «Онхойская основная школа
  имени С.П.Федотова”.
  Учитель информатики: Васильев А.Н.

• 

  2 слайд

  Содержание
  Данные, величина, команды
  Постоянная и переменная величина
  Характеристика величины
  Понятие «алгоритм»
  Исполнитель алгоритма
  СКИ
  Свойства алгоритма
  Линейный алгоритм
  Разветвляющийся алгоритм
  Циклический алгоритм
  Понятие «цикл»

• 

  3 слайд

  Всё, что бы мы ни делали, чаще всего имеет какую-либо цель. И не всегда эта цель достигается.
  Если точно и правильно сформулировать желаемый результат, а потом продумать чёткий план его содержания, то эта цель будет достигнута

  начало

• 

  4 слайд

  Данные – это информация, обрабатываемая компьютером.

  Величина – это отдельная единица данных.

  Команды — позволяют определить действия в компьютерной программе над величинами.
  начало

• 

  5 слайд

  По отношению к программе данные могут быть
  исходные
  промежуточные
  результаты
  начало

• 

  6 слайд

  Постоянная величина – величина, значение которой не изменяется в процессе исполнения алгоритма, а остается одним и тем же, указанным в тексте алгоритма.

  Переменная величина — величина, значение которой меняется в процессе исполнения алгоритма.
  начало

• 

  7 слайд

  Характеристики величины:
  Имя (идентификатор) — это обозначение величины и место в памяти.
  Тип — множество допустимых значений и множество применимых операций к величине.
  Значение — характеристика, может меняться многократно в ходе исполнения алгоритма.
  начало

• 

  8 слайд

  Алгоритм –
  это последовательность действий, приводящая к достижению результата

  начало

• 

  9 слайд

  В определении «алгоритм» содержатся основные понятия, связанные с ним и его главные свойства
  Данные
  Исполнитель
  Результаты
  Алгоритм:
  1-ая команда
  2-ая команда
  ………………..
  N-ая команда
  Данные
  Взаимосвязь понятий:
  начало
  inppt.ru

• 

  10 слайд

  Исполнитель
  Центральным объектом в схеме является Исполнитель – это тот объект (или субъект) для управления которым составляется алгоритм
  начало

• 

  11 слайд

  СКИ
  Основной характеристикой исполнителя, с точки зрения управления, является система команд исполнителя (СКИ) — это конечное множество команд, которые понимает исполнитель, т.е. умеет их выполнять

  начало

• 

  12 слайд

  Для выполнения всякой работы, решения поставленной задачи исполнитель на входе получает алгоритм и исходные данные, а на выходе — требуемые результаты. Алгоритм может включать в себя только команды,
  входящие в СКИ

• 

  13 слайд

  Свойства алгоритмов:
  Результативность (или конечность) – выполнение алгоритма должно приводить к результату за конечное число шагов;
  Дискретность (или детализация) – алгоритм поддаётся расчленению на элементарные (дискретные) шаги, которые могут быть исполнены при помощи системы команд исполнителя;
  начало

• 

  14 слайд

  Свойства алгоритмов:
  Однозначность – каждый шаг исполнителя может и должен быть истолкован одним и только одним способом;
  Понятность – алгоритм должен быть составлен только из команд, входящих в систему команд исполнителя;

  начало

• 

  15 слайд

  Свойства алгоритмов:
  Массовость – алгоритм должен решать однотипные задачи с различными исходными данными;
  Переносимость
  (или совместимость) – алгоритм не должен зависеть от типа используемой вычислительной техники или выбранного языка программирования;
  начало

• 

  16 слайд

  Виды алгоритмов
  Существует три основных вида алгоритмов, которые и являются базовыми при написании программ

• 

  17 слайд

  Линейный алгоритм – это алгоритм, в котором все действия выполняются в строгом порядке, последовательно, одно за другим
  Первый тип алгоритмов
  Например: включение персонального компьютера
  начало

• 

  18 слайд

  Алгоритм, в котором осуществляется выбор действий в зависимости от какого-то условия, называют разветвляющимся
  Второй тип алгоритма
  начало

• 

  19 слайд

  Настроение
  хорошее?
  Позвонить другу
  Погулять
  ДА
  НЕТ
  НАЧАЛО
  КОНЕЦ
  ДА
  НЕТ
  ДА
  НЕТ
  Пример разветвляющегося алгоритма

• 

  20 слайд

  Третий тип алгоритмов
  Циклический алгоритм –
  это алгоритм, содержащий повторяющие действия с какой–либо изменяющейся величиной (параметром)
  начало

• 

  21 слайд

  Повторяющаяся последовательность действий называется циклом,

  а эти действия – циклическими

  начало

• 

  22 слайд

  НАЧАЛО
  Ягоды
  собраны?
  Сорви ягоду
  Положи в корзину
  Унеси корзину
  КОНЕЦ
  ДА
  ДА
  НЕТ
  НЕТ
  НЕТ
  Пример циклического алгоритма

Краткое описание документа:

Алгоритм — точное предписание исполнителю совеpшить определенную последовательность действий для достижения поставленной цели за конечное число шагов.

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi – латинского написания имени Мухаммеда аль-Хорезми (787 – 850) выдающегося математика средневекового Востока. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных.

Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, — процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.

Данное выше определение алгоритма нельзя считать строгим – не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата».

Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.

Такими свойствами являются:

• Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.

• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

На основании этих свойств иногда дается определение алгоритма, например: “Алгоритм – это последовательность математических, логических или вместе взятых операций, отличающихся детерменированностью, массовостью, направленностью и приводящая к решению всех задач данного класса за конечное число шагов”.

Такая трактовка понятия “алгоритм” является неполной и неточной.

Во-первых, неверно связывать алгоритм с решением какой-либо задачи. Алгоритм вообще может не решать никакой задачи.

Во-вторых, понятие “массовость” относится не к алгоритмам как к таковым, а к математическим методам в целом. Решение поставленных практикой задач математическими методами основано на абстрагировании – мы выделяем ряд существенных признаков, характерных для некоторого круга явлений, и строим на основании этих признаков математическую модель, отбрасывая несущественные признаки каждого конкретного явления. В этом смысле любая математическая модель обладает свойством массовости. Если в рамках построенной модели мы решаем задачу и решение представляем в виде алгоритма, то решение будет “массовым” благодаря природе математических методов, а не благодаря “массовости” алгоритма.

Виды алгоритмов

Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:

• Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т.п.);

• Гибкие алгоритмы, например стохастические, т.е. вероятностные и эвристические. Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.

• Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.

• Эвристический алгоритм (от греческого слова “эврика”) – это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.

• Линейный алгоритм – набор команд (указаний), выполняемых последовательно во времени друг за другом.

• Разветвляющийся алгоритм – алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.

• Циклический алгоритм – алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов.

Цикл программы – последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторого условия.

Вспомогательный (подчиненный) алгоритм (процедура) – алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм.

На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.

Структурная (блок-, граф-) схема алгоритма – графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков – графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия.

Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации.

Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему – набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации “. Здесь форма представления алгоритма смешивается с самим алгоритмом.

Требования, предъявляемые к алгоритму

Первое правило – при построении алгоритма прежде всего необходимо задать множество объектов, с которыми будет работать алгоритм. Формализованное (закодированное) представление этих объектов носит название данных. Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные. Это правило позволяет сразу отделить алгоритмы от “методов” и “способов”. Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.

Второе правило – для работы алгоритма требуется память. В памяти размещаются входные данные, с которыми алгоритм начинает работать, промежуточные данные и выходные данные, которые являются результатом работы алгоритма. Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной. В теории алгоритмов размеры памяти не ограничиваются, т. е. считается, что мы можем предоставить алгоритму любой необходимый для работы объем памяти. В школьной “теории алгоритмов” эти два правила не рассматриваются. В то же время практическая работа с алгоритмами (программирование) начинается именно с реализации этих правил.

В языках программирования распределение памяти осуществляется декларативными операторами (операторами описания переменных). В языке Бейсик не все переменные описываются, обычно описываются только массивы. Но все равно при запуске программы транслятор языка анализирует все идентификаторы в тексте программы и отводит память под соответствующие переменные.

Третье правило – дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). Множество шагов, из которых составлен алгоритм, конечно.

Четвертое правило – детерменированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки. Пятое правило – сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 221 581 материал в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы