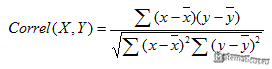Корреляционный анализ в spss пошаговая инструкция

Глава 15. Корреляционный анализ

• 15.1. Коэффициент корреляции Пирсона
• 15.2. Ранговые коэффициенты корреляции по Спирману и Кендалу
• 15.3. Частная корреляция
• 15.4. Мера расстояния и мера сходства
• 15.5. Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))

Корреляция — связь между двумя переменными. Расчёты подобных двумерных критериев взаимосвязи основываются на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок.

Если в качестве примера возьмём данные об уровне холестерина для первых двух моментов времени из исследования гипертонии (файл hyper.sav),
то в данном случае следует ожидать довольно сильную связь: большие значения в исходный момент времени являются веским поводом для ожидания больших значений и через 1 месяц.

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным.
Каждая пара значений маркируется при помощи определенного символа. Такой график, называемый «диаграммой рассеяния» (Scatterplot) для двух зависимых переменных можно построить путём вызова меню
Graphs… (Графики) / Scatter plots… (Диаграммы рассеяния) (см. гл. 22.8).

Образовавшееся скопление точек показывает, что обследованные пациенты с высокими исходными показателями, как правило, имеют высокие значения холестерина и при повторном опросе через месяц.

Статистика говорит о корреляции между двумя переменными и указывает силу связи при помощи некоторого критерия взаимосвязи, который получил название коэффициента корреляции.
Этот коэффициент, всегда обозначаемый латинской буквой r, может принимать значения между -1 и +1, причём если значение находится ближе к 1, то это означает наличие сильной связи,
а если ближе к 0, то слабой.

Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой.
Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следуюшие градации:

Значение	Интерпретация
до 0,2	Очень слабая корреляция
до 0,5	Слабая корреляция
до 0,7	Средняя корреляция
до 0,9	Высокая корреляция
свыше 0,9	Очень высокая корреляция

Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные:

Типы шкал	Мера связи
Переменная X	Переменная Y
Интервальная (или отношений)	Интервальная (или отношений)	Коэффициент Пирсона
Ранговая, интервальная (или отношений)	Ранговая, интервальная (или отношений)	Коэффициент Спирмена
Ранговая	Ранговая	Коэффициент Кендалла
Дихотомическая	Дихотомическая	Коэффициент φ (фи), четырёхполевая корреляция
Дихотомическая	Ранговая	Рангово-бисериальный коэффициент

• Переменные с интервальной или с пропорциональной шкалой – коэффициент корреляции Пирсона.

• По меньшей мере, одна из двух переменных имеет порядковую шкалу, либо с интервальной шкалой, но не нормально распределённой – ранговая корреляция по Спирману или
  τ (тау-грого-соая) Кендала (реже).

• Одна из двух переменных является дихотомической – точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применён расчёт ранговой корреляции по Спирману.

• Обе переменные являются дихотомическими – четырёхполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства (см. гл 15.4).

Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю.
В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Ешё один раздел специально посвящён частной корреляции.

---

Матрица корреляции — это квадратная таблица, которая показывает коэффициенты корреляции Пирсона между различными переменными в наборе данных.

Напомним, чтокоэффициент корреляции Пирсона — это мера линейной связи между двумя переменными . Он принимает значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
• 0 указывает на отсутствие линейной корреляции между двумя переменными
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.

В этом руководстве объясняется, как создать и интерпретировать корреляционную матрицу в SPSS.

Пример: Как создать матрицу корреляции в SPSS

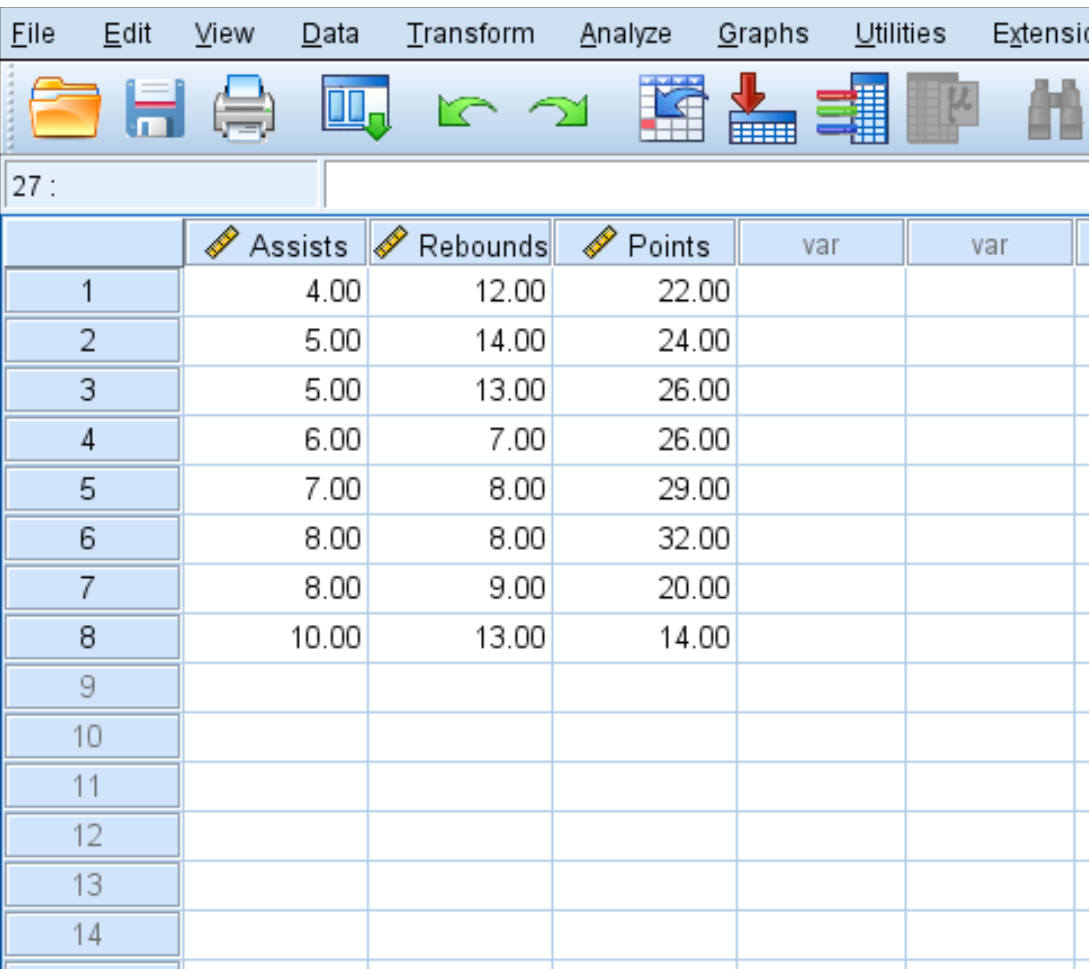
Используйте следующие шаги, чтобы создать матрицу корреляции для этого набора данных, которая показывает средние передачи, подборы и очки для восьми баскетболистов:

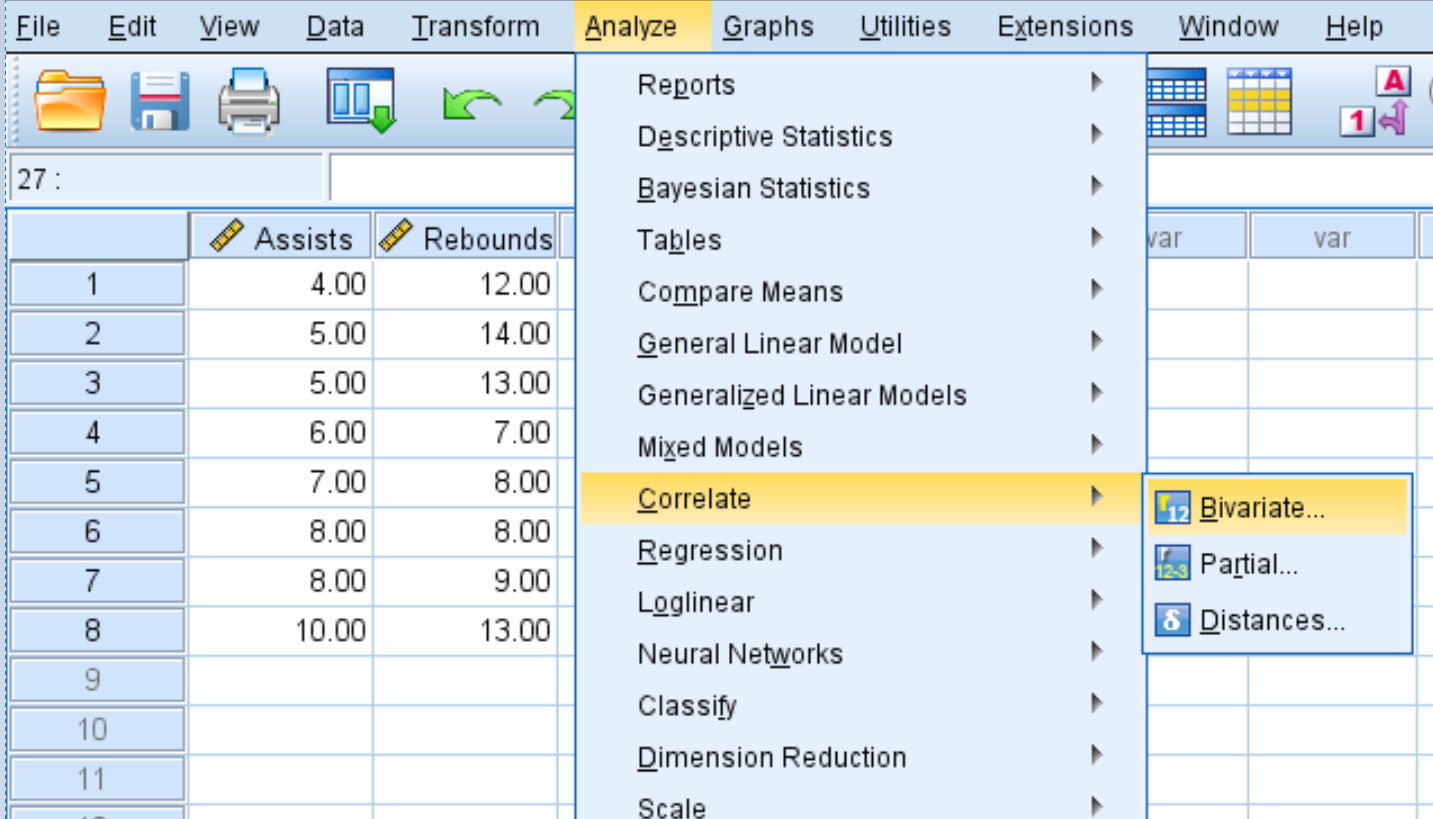
Шаг 1: Выберите двумерную корреляцию.

• Щелкните вкладку Анализ .
• Щелкните Сопоставить .
• Щелкните Двумерный .

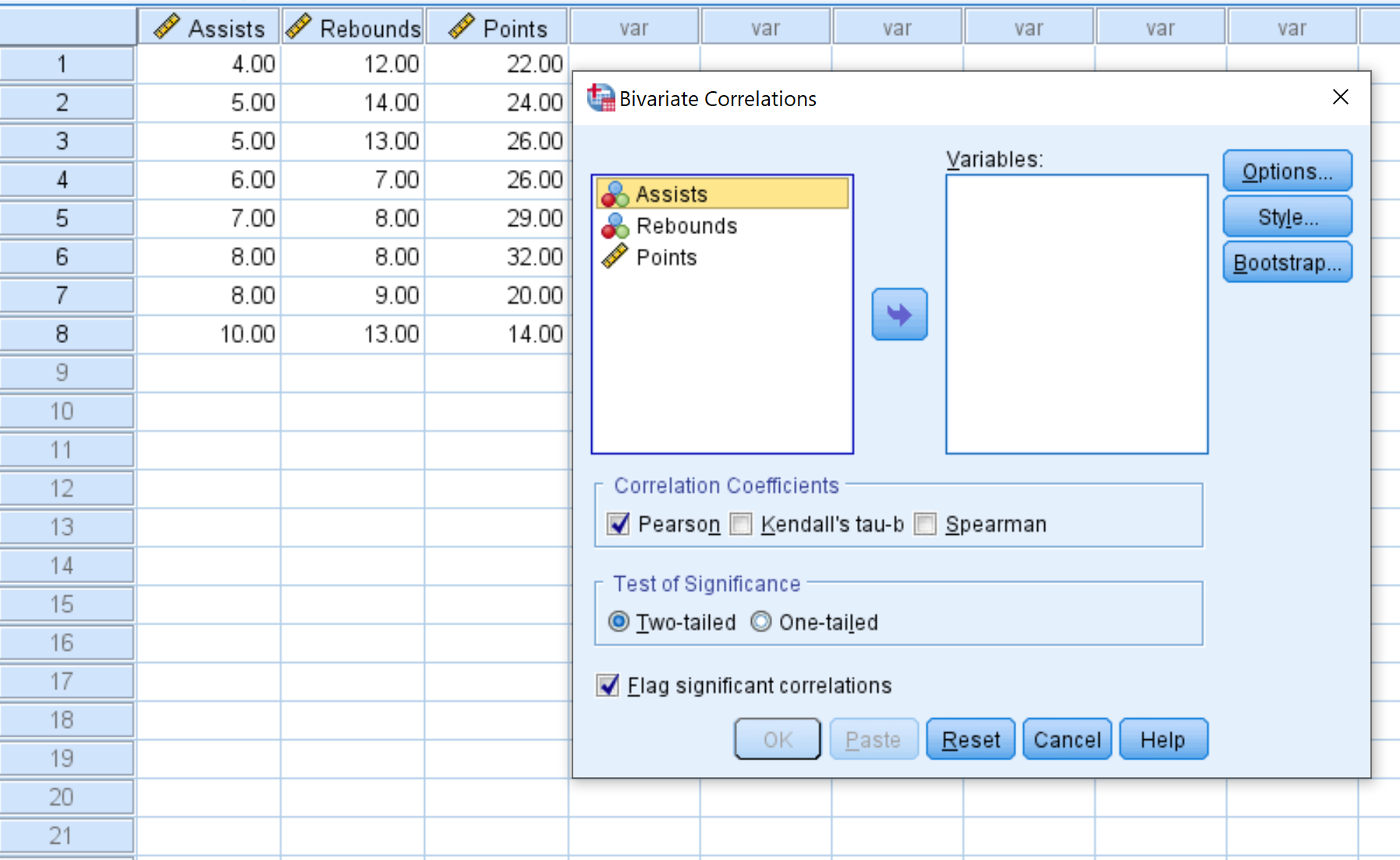
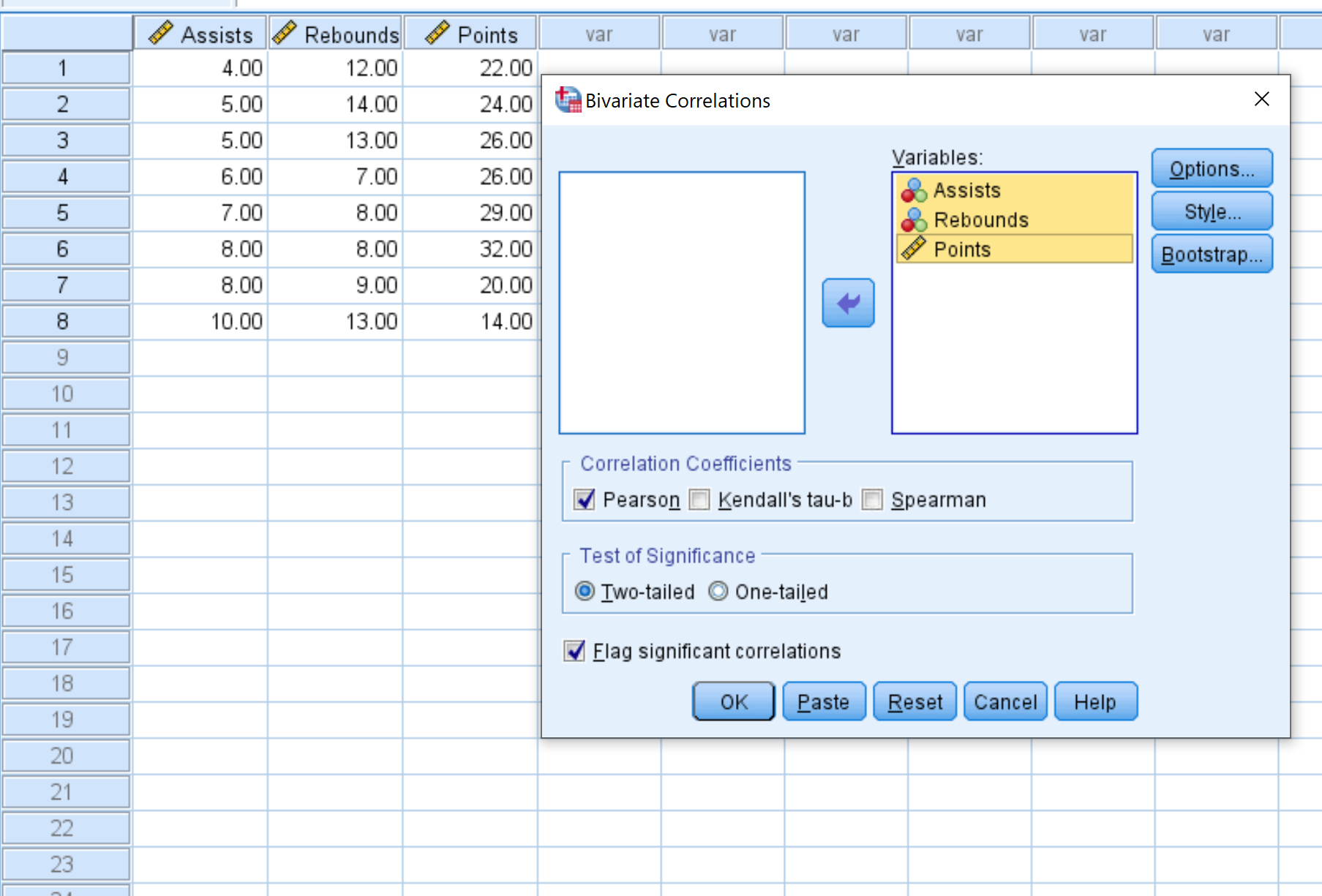
Шаг 2: Создайте матрицу корреляции.

Каждая переменная в наборе данных первоначально будет показана в поле слева:

• Выберите каждую переменную, которую вы хотите включить в матрицу корреляции, и щелкните стрелку, чтобы перенести их в поле « Переменные ». В этом примере мы будем использовать все три переменные.
• В разделе Коэффициенты корреляции выберите, хотите ли вы использовать корреляцию Пирсона, тау Кендалла или Спирмена. Мы оставим его как Pearson для этого примера.
• В разделе Проверка значимости выберите, следует ли использовать двусторонний или односторонний тест, чтобы определить, имеют ли две переменные статистически значимую связь. Мы оставим его как Двухвостого.
• Установите флажок рядом с Отметить существенные корреляции , если вы хотите, чтобы SPSS помечал переменные со значительной корреляцией.
• Наконец, нажмите ОК .

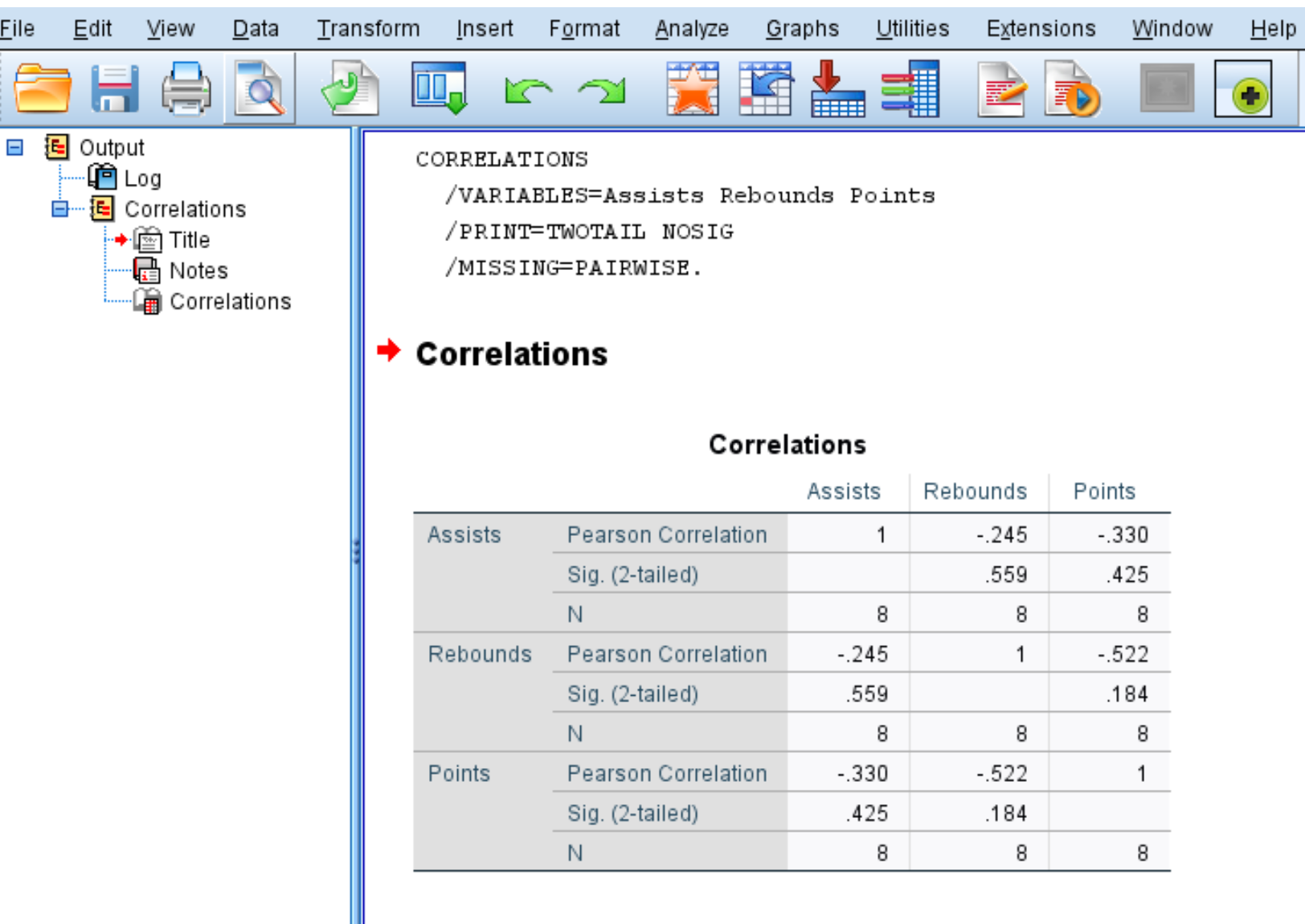
После того, как вы нажмете OK , появится следующая матрица корреляции:

Шаг 3: Интерпретируйте матрицу корреляции.

Матрица корреляции отображает следующие три показателя для каждой переменной:

• Корреляция Пирсона: мера линейной связи между двумя переменными в диапазоне от -1 до 1.
• Сиг. (2-стороннее): двустороннее значение p, связанное с коэффициентом корреляции. Это говорит вам, имеют ли две переменные статистически значимую связь (например, если p < 0,05).
• N: количество пар, используемых для расчета коэффициента корреляции Пирсона.

Например, вот как интерпретировать вывод переменной Assists:

• Коэффициент корреляции Пирсона между передачами и подборами составляет -0,245.Поскольку это число отрицательное, это означает, что эти две переменные имеют отрицательную связь.
• Значение p, связанное с коэффициентом корреляции Пирсона для передач и подборов, составляет 0,559.Поскольку это значение не менее 0,05, две переменные не имеют статистически значимой связи.
• Количество пар, использованных для расчета коэффициента корреляции Пирсона, равнялось 8 (например, в этом расчете использовалось 8 пар игроков).

Шаг 4: Визуализируйте матрицу корреляции.

Вы также можете создать матрицу диаграммы рассеяния, чтобы визуализировать линейную зависимость между каждой из переменных.

• Щелкните вкладку Графики .
• Нажмите Построитель диаграмм .

• Чтобы выбрать тип диаграммы, щелкните Точечная/точечная .
• Щелкните изображение с надписью Матрица рассеяния .
• В поле « Переменные » в левом верхнем углу, удерживая Ctrl, щелкните все три имени переменных. Перетащите их в поле в нижней части диаграммы с надписью Scattermatrix .
• Наконец, нажмите ОК .

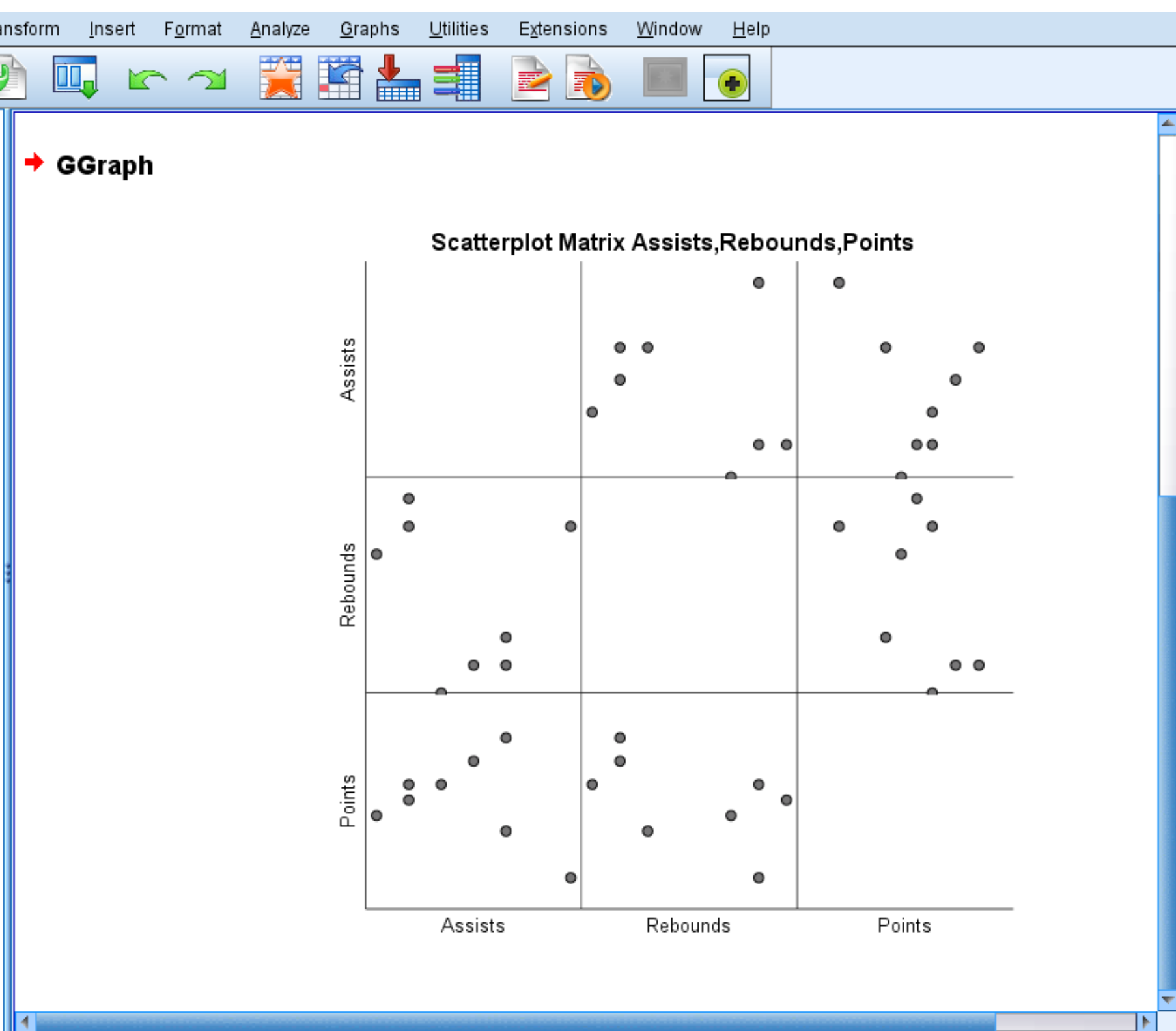
Автоматически появится следующая матрица диаграммы рассеяния:

Каждая отдельная диаграмма рассеяния показывает попарные комбинации между двумя переменными. Например, диаграмма рассеяния в левом нижнем углу показывает попарные комбинации очков и передач для каждого из 8 игроков в наборе данных.

Матрица диаграммы рассеяния не является обязательной, но она предлагает хороший способ визуализировать взаимосвязь между каждой парной комбинацией переменных в наборе данных.

Для того, чтобы рассчитать коэффициент корреляции используя статистический пакет SPSS необходимо сделать следующие шаги:

1.Вносим значения для двух переменных в таблицу Data Editor. (Например var1 и var2)

2. Выбираем Analyze -> Correlate -> Bivariate…

3. В открывшемся окне выделяем две переменные (например var1 и var2).

4. Нажимаем на кнопку >. Выделенные переменные перенесутся вправо, в окно Paired Variables (они будут выглядеть как var1-var2).

5. Выделяем нужный метод вычисления коэффициента корреляции:

• корреляцию Пирсона (Pearson) — стоит по-умолчанию
• корреляцию r-Спирмена (Spearman)
• корреляцию t-Кендала (Kendal)

5.1.Если необходимо учесть пропуски значений путем их построчного удаления, то нажимаем Options -> Exclude cases listwise -> Continue. По-умолчанию программа использует учет пропусков значений путем их попарного удаления (Exclude cases pairwise).

6. Нажимаем Ок

7. Смотрим полученный результат

Задание 2.4.

Произвести анализ
зависимости объема продаж товара от
затрат на рекламу данного товара. Данные
приведены в табл. 2.4.1.

Таблица 2.4.1

Затраты на рекламу, тыс. руб.	110	113	115	116	221	226	332	333	339	442
Объемы продаж, тыс. руб.	410	415	410	425	439	460	485	473	489	491

Выполнение.

В начале работы
создадим файл с данными как показано
на рис. 2.4.1.

Рис. 2.4.1. Фрагмент
файла данных

В пакете SPSS
для корреляционного анализа есть раздел
«Корреляция в меню. Анализ».

Для более наглядного
представления имеющихся данных построим
график зависимости «Затраты на рекламу
– объем продаж» в виде диаграммы
рассеяния.

• Выберем в меню
  Graphs
  (Визуализация) Scatter–Dot
  (Разброс/точка), откроется диалоговое
  окно Scatter–Dot
  (Разброс/точка) (рис. 2.4.2).

Рис. 2.4.2. Диалоговое
окно Scatter–Dot
(Разброс/точка)

• В диалоговом окне
  Scatter–Dot
  (Разброс/точка) щёлкнем на области
  Simple Scatter
  (Простой разброс).

• Щелчком по
  выключателю Define
  (Определить) откроем соответствующее
  диалоговое окно (рис. 2.4.3).

• Отобразим объем
  продаж в зависимости от затрат на
  рекламу, поэтому переменную объемы_продаж
  из списка исходных переменных перенесем
  в поле оси Y,
  а переменную затраты_на_рекламу
  – в поле оси X.
  И начнем построение диаграммы щелчком
  на ОК.

Результатом
выполнения вышеуказанных команд будет
следующий график (рис. 2.4.4).

Рис. 2.4.3. Вид окна
Simple Scatterplot
(Простой график рассеяния).

Рис. 2.4.4. Простой
график рассеивания

Теперь определим
основные корреляционные показатели.

Для этого в меню
Анализ выбираем Корреляция – Двумерный.

Далее появится
диалоговое окно (рис. 2.4.5).

Рис. 2.4.5. Диалоговое
окно «Двумерная корреляция»

Далее получаем
следующий вывод (рис.2.4.6).

Регрессионный
анализ служит для определения вида
связи между переменными и дает возможность
для прогнозирования значения одной
(зависимой) переменной отталкиваясь от
значения другой (независимой) переменной.

В пакете SPSS
для этой цели имеется раздел Regression
(Регрессия) (меню Analyze
(Анализ)), который предоставляет
пользователю широкий набор процедур
регрессионного анализа.

Каждая процедура
имеет модель регрессии, которая соотносит
зависимую переменную с независимой
переменной (или множеством независимых
переменных).

Простая линейная
регрессия лучше всего подходит для
того, чтобы продемонстрировать
основополагающие принципы регрессионного
анализа.

По виду получившейся
диаграммы рассеяния можно предположить
о наличии линейной зависимости между
исследуемыми показателями.

Описательные
статистики

	Среднее	Стд. отклонение	N
затраты_на_рекламу	24,7000	11,37297	10
объем_продаж	450,6000	32,63332	10

Корреляции(a)

		затраты_на_рекламу	объем_продаж
затраты_на_рекламу	Корреляция Пирсона	1	,983(**)
	Знч.(1–сторон)		,000
объем_продаж	Корреляция Пирсона	,983(**)	1
	Знч.(1–сторон)	,000

**
Корреляция значима на уровне 0.01
(1–сторон.).

a Искл. целиком
N=10

Корреляции(a)

		затраты_на_рекламу	объем_ продаж
тау–b Кендалла	затраты_на_рекламу	Коэффициент корреляции	1,000	,956(**)
		Знч. (1–сторон)	.	,000
	объем_продаж	Коэффициент корреляции	,956(**)	1,000
		Знч. (1–сторон)	,000	.
ро Спирмена	затраты_на_рекламу	Коэффициент корреляции	1,000	,988(**)
		Знч. (1–сторон)	.	,000
	объем_продаж	Коэффициент корреляции	,988(**)	1,000
		Знч. (1–сторон)	,000	.

**
Корреляция значима на уровне 0.01
(1–сторонняя).

a Искл. целиком N
= 10

Рис.
2.4.6. Вывод корреляций

Перейдем к построению
регрессионной зависимости между
показателями.

• Выберем в меню
  Analyze
  (Анализ) Regression
  (Регрессия) Linear
  (Линейная). Появится диалоговое окно
  Linear Regression
  (Линейная регрессия) (рис. 2.4.7).

Рис. 2.4.7. Вид
диалогового окна Linear
Regression
(Линейная регрессия)

• Перенесем переменную
  объемы_продаж
  в поле для зависимых переменных и
  присвоим переменной затраты_на_рекламу
  статус независимой переменной.

• Ничего больше не
  меняя, начните расчёт нажатием ОК.

Вывод основных
результатов выглядит следующим образом
(рис. 2.4.8).

Во второй таблице
дается заключение о соответствии модели
исходным данным, а именно приводится
коэффициент детерминации, который
характеризует качество получившейся
модели.

В третьей таблице
приведены величины, которые отражают
два источника дисперсии: дисперсию,
которая описывается уравнением регрессии
(сумма квадратов, обусловленная
регрессией) и дисперсию, которая не
учитывается при записи уравнения
(остаточная сумма квадратов). Также
приведено значение F–критерия
Фишера.

В последней таблице
выводятся коэффициент регрессии b
и смещение по оси ординат а
под именем «константа».

То есть, уравнение
регрессии выглядит следующим образом:

,

где
показатель «Объемы продаж»,показатель «Затраты на рекламу».

Включенные/исключенные
переменные(b)

Модель	Включенные переменные	Исключенные переменные	Метод
1	затраты_на_рекламу(a)	.	Принудительное включение

a Включены все
запрошенные переменные

b Зависимая
переменная: объем_продаж

Сводка для модели

Модель	R	R квадрат	Скорректированный R квадрат	Стд. ошибка оценки
1	,983(a)	,966	,962	6,39137

a Предикторы:
(константа) затраты_на_рекламу

Дисперсионный
анализ (b)

Модель		Сумма квадратов	ст.св.	Средний квадрат	F	Знч.
1	Регрессия	9257,603	1	9257,603	226,627	,000(a)
	Остаток	326,797	8	40,850
	Итого	9584,400	9

a Предикторы:
(константа) затраты_на_рекламу

b Зависимая
переменная: объем_продаж

Коэффициенты(a)

Модель	Нестандартизованные коэффициенты	Станд. коэфф.	t	Знч.
	B	Стд. ошибка	Бета
1	(Константа)	380,945	5,049		75,448	,000
	затраты_на_рекламу	2,820	,187	,983	15,054	,000

a Зависимая
переменная: объем_продаж

Рис. 2.4.8. Результат
выполнения процедуры Analyze
– Regression
– Linear

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Skip to content

Рассмотрим корреляционный анализ в программе SPSS Statistics

Даны данные:
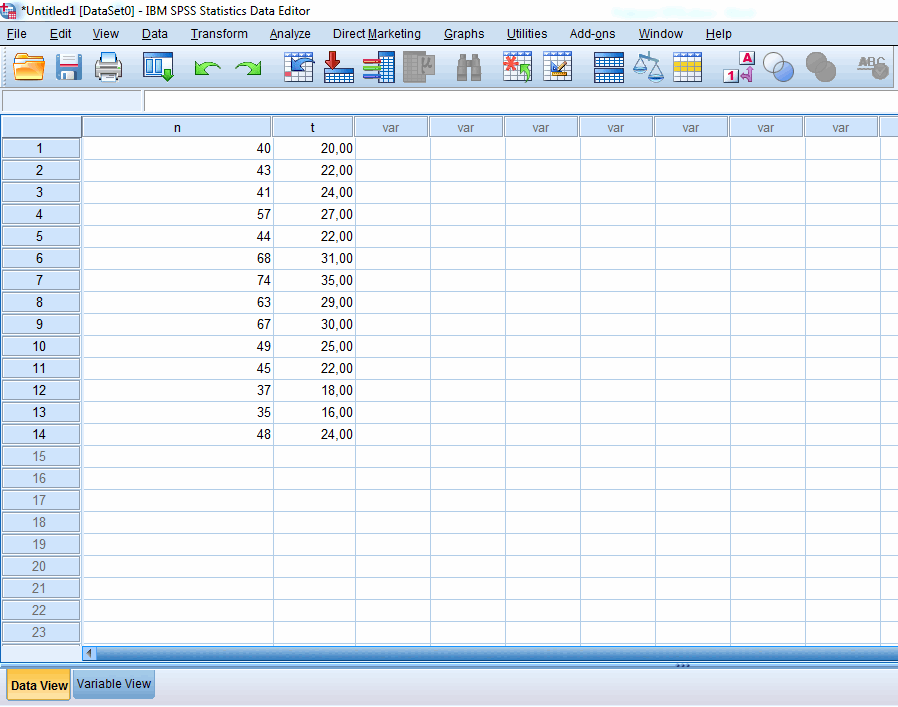
n — количество купленного мороженого в магазине;
t —   температура воздуха.

Рисунок 1 – Вводим в программу количественные данные показателей n и t

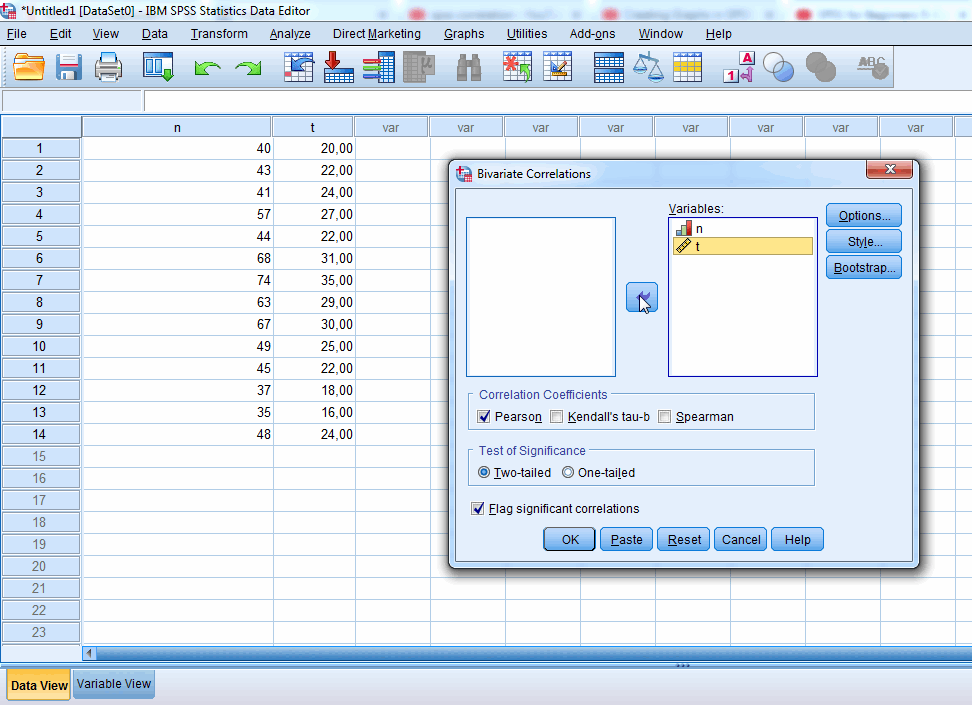
Рисунок 2 – Переходим на вкладку Analyze -> Correlate -> Bivariate, то есть выбираем корреляционный анализ

Рисунок 3 — Выбираем исходные значения n и t

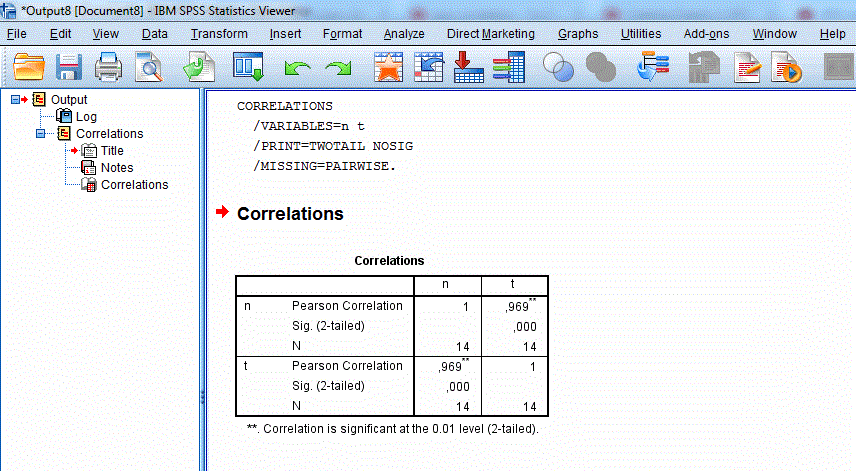
Рисунок 4 – Получаем отчёт в программе SPSS Statistics в виде значения коэффициента корреляции. В нашем случае он равен 0.969 Это говорит о том, что величины связаны друг с другом сильно.

Коэффициент корреляции находится по формуле:

1624