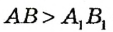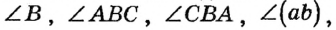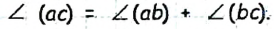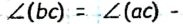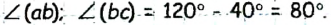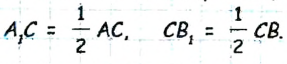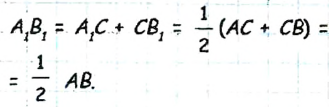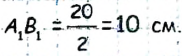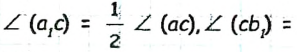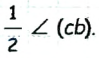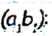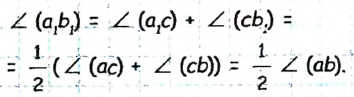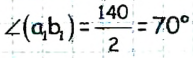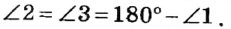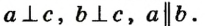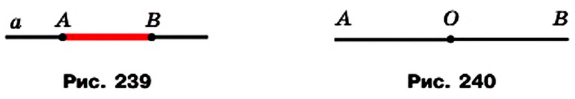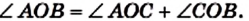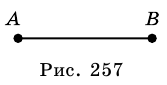Как рисовать геометрические фигуры на плоскости
Правильный рисунок геометрической фигуры к задаче по геометрии – почти половина решения задачи.
Да-да, настолько он важен!
При правильном построении он поможет тебе не запутаться в данных и увидеть новые детали!
И сейчас ты научишься изображать объемные геометрические фигуры на плоскости. Это очень важно в стереометрии.
Поехали!
Как нарисовать пространственную фигуру так, чтобы было видно, что она объемная?
Есть несколько правил, применяя которые, ты всегда будешь получать красивые и понятные чертежи к своим задачам. Итак:
Как рисовать линии в трехмерном пространстве
Все линии (ребра, высоты, линии сечения), которые были бы не видны, если бы то, что мы рисуем, было бы сделано из глины (например) изображаются пунктиром. А все видные линии – сплошными.
Вот, смотри на несколько уже готовых чертежей, и поймешь, о чем речь.
Но возникает вопрос: а как вообще дойти до готового чертежа, где что-то должно быть сплошным, а что-то пунктиром?
Следующие правила как раз об этом.
Как рисовать квадраты и прямоугольники объемными
Все квадраты и прямоугольники, которые лежат в горизонтальной плоскости, нужно изображать параллелограммами, а прямоугольные треугольники – с острым углом, вместо прямого.
Видишь, похоже, будто треугольники прямоугольник лежат в плоскости.
Круги на плоскости
Все круги превращаются в овалы (тоже в горизонтальной плоскости)
Пирамида на плоскости
Когда рисуешь треугольную пирамиду, нужно сперва нарисовать «косой» четырехугольник:
А потом добавить еще два ребра:
И никогда ничего не сольется! Можно смело проводить высоту и строить сечения:
С четырехугольной пирамидой сложнее, но тоже разумно сперва прорисовать контур, а потом добавлять ребра.
Но только в исходном четырехугольнике одна из сторон должна быть параллельна взгляду:
А потом проводим параллельные:
И осталось только соединить:
Получилась красивая пирамида – Хеопс тоже не отказался бы 🙂
И осталось самое сложное – шестиугольная пирамида.
Чаще всего нужна правильная. Здесь уже сперва основание! Но…как мне нарисовать правильный шестиугольник, чтобы было похоже, что он лежит? Его нужно нарисовать приплюснутым (но соблюдая все параллельности: ( left( AB||ED; BC||FE; AF||CD; BE||CD right))
Потом из центра основания провести перпендикуляр, чтобы легче найти вершину.
И потом уже соединить вершину с вершинами основания.
И не думай, что шестиугольная пирамида получится с первого раза – нужно тренироваться!
Параллелепипед на плоскости
Тут сперва нужно нарисовать основание в виде параллелограмма:
Потом одну боковую грань:
А потом все остальные – и главное – соблюдать параллельность.
Призма на плоскости
Если нужно изобразить треугольную призму, то рисовать нужно так, чтобы угол треугольника смотрел на нас – живее получится. Вот:
А затем боковые ребра:
И потом верхнее основание:
Шар на плоскости
Сначала рисуем круг:
А потомобавим две дуги, чтобы получился такой овал с острыми краями. И ставим центр.
Цилиндр на плоскости
Рисуем овал и отмечаем его центр:
Проводим две образующие:
И “закрываем” верхним основанием. Обрати внимание на то, как расположены центры верхнего и нижнего овалов.
Рисуем на плоскости конус
Рисуем овал:
И делаем угол:
Обрати внимание: образующие (стороны угла) касаются основания, поэтому центр основания и две точки на нём не лежат на одной прямой (в отличие цилиндра).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
В статье описываются геометрические фигуры: определение, основные свойства и формулы.
Плоские геометрические фигуры:
-
Четырехугольник (общее для всех четырехугольников)
-
Квадрат
-
Прямоугольник
-
Параллелограмм
-
Ромб
-
Трапеция
-
Треугольник
-
Окружность
Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные
.
Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Что такое точка?
Как только маленький ребенок берет в ручки карандаш, он уже замечательно умеет рисовать геометрическую фигуру. Какую? – удивитесь вы. Это точка.
Точка – наименьшая, простейшая фигура геометрии, никак не измеряется.
И строить её умеет даже маленький ребенок.
Обозначать точки в математике, принято большими буквами латиницы.
Произносится:точка А, точка В, точка С.
Следующее понятие, которое мы рассмотрим, знакомо каждому с самого детства. Нет ничего проще, чем нарисовать прямую линию. Многие успешно рисовали их на новых обоях, мебели. А оказывается – она одна из основных фигур геометрии.
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона Площадь: S=a2или S=d2/2 Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2 Радиус описанной окружности: R=d или R=a/√(2) Радиус вписанной окружности: r=a/2
где a-сторона, d-диагональ, P-периметр, S-площадь *Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2Площадь по сторонам: S = a*bПлощадь по диагонали и углу между ними: S = d²* sin γ. / 2Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора) Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)
где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь γ – угол между диагоналями*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
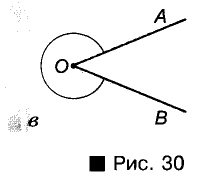
Что такое вершина и стороны угла?
Точка называется вершиной угла, лучи– сторонами угла. Обозначают строчными, заглавными буквами латиницы (отметив на сторонах дополнительные точки). Для письменного обозначенияиспользуется специальный знак ∠.
Записывается, читается:∠β – угол бета,∠BAС – угол BAС.
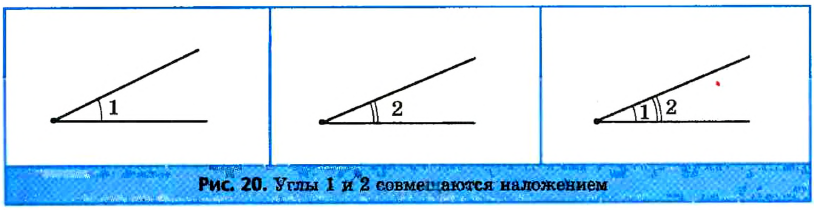
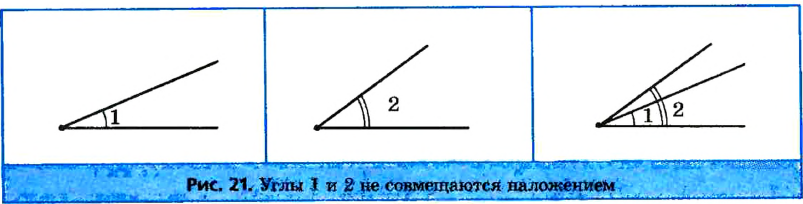
Углы равны, если при наложении они совпадают.
Мы наложили ∠BAС на ∠ β,при совмещении, у них совпали (полностью совместились) вершины, стороны углов. Значит ∠BAС=∠ β.
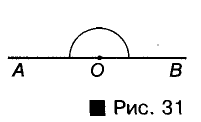
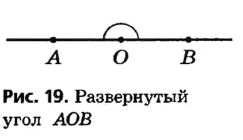
Бывают случаи, когда източки выходят два луча в противоположные стороны, образуя при этом прямую линию. Например:
Полученная фигура называется развернутым углом.
Развернутый угол – фигура, стороны которой, дополняя друг друга, создают прямую линию. Градусная мера угласоставляет 180 ˚.
Все углы принято измерять градусами. Градус–единица измерения углов, составляет 1/180 часть развернутого угла. Для письменного обозначения градуса используется специальный символ – ˚.
Получается, что∠ α=180 ˚.
Читается как: градусная мера развернутого угла альфа равна 180 градусам.
Если такой угол разделить пополам, то получим 2 равнозначных угла.
Рассмотрим развернутый ∠ВАС. Луч АО делит ∠ВАС пополам, чтобы узнать градусную меру полученных углов, необходимо градусную меру развернутого угла, поделить пополам (180:2=90). Получается, что ∠ОАС и ∠ВАО имеют градусную меру равную 90 ˚, называются прямыми углами.
Прямым углом называют половину развернутого угла, градусная мера которого составляет 90 ˚
Ну, а теперь, можете попросить у родителей чашку горячего чая. Ведь для изучения следующего определения, будем использовать вкусный, ароматный бублик.
Бублик – лакомство, знакомое с самого детства. Но вряд ли кто-то из вас задумывался какую форму имеет любимая выпечка? Если рассматриватьс геометрической точки зрения, то бублик представляетзамкнутую линию теста, все точки которой лежат на одинаковом расстоянии от центра изделия. В геометрии такая фигура называется окружностью.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1)2+(d2)2=(a2+b2)*2 Периметр: P=(a+b)*2 Площадь по стороне и высоте: S =a*h S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α S (Площадь) по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
где a, b — длины сторон, d1, d2 –диагонали, P-периметр, S-площадь, h-высота, проведенная к противоположной стороне α — угол между сторонами параллелограмма, γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
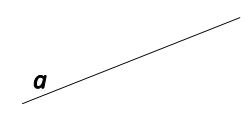
Что такое прямая?
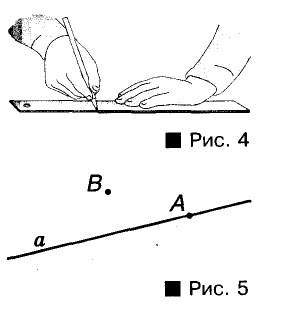
Прямая – масса точек, находящихся на общей, бесконечной линии. Обозначается прописными буквами латиницы.
Произносится: прямая а.
Через выбранные 2 точки можно провести одну-единственную прямую!
Через точки Р, К, проводится только 1 прямая.
Все очень просто!
Теперь предлагаю нарисовать солнышко.
Давайте рассмотрим его поподробнее. Солнышко состоит из круга, лучиков. Вот мы подошли к следующему понятию геометрии.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*aПлощадь по стороне и высоте: S=a*h Площадь по диагоналям: S = (d1*d2)/2 Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a Площадь по стороне и радиусу вписанной окружности: S=2*a*rПлощадь по стороне и углу: S = a2 · sin α
где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь, h -высота, проведенная к противоположной стороне α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d Площадь определить: S=h*(a+b)/2 Стороны и диагональ равнобокой трапеции: d² = ab+c²Радиус вписанной окружности: r = h/2
где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали, P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c Площадь по стороне и высоте: S=(a*h)/2 Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r Площадь прямоугольного треугольника: S=(a*b)/2Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника) d1, d2 –диагонали, h -высота, проведенная к противоположной стороне, P-периметр, S-площадь, γ — угол между сторонами a и b r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b|
- Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
- Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
- В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
- Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Изучение геометрических фигур: названия, форма, цвет, размер
С простыми фигурами и их цветами детей знакомят с 2 до 3 лет. Обучение должно происходить ненавязчиво, в форме рассказа или развлечения.
На помощь могут прийти:
- сортер;
- игрушки с деревянными вкладышами;
- картинки.
- белый;
- зеленый;
- желтый;
- красный;
- синий;
- розовый;
- черный;
- фиолетовый;
- оранжевый;
- круг;
- квадрат;
- треугольник;
- овал;
- прямоугольник;
- полукруг.
Геометрические фигуры объемные можно и необходимо изучать в игровой форме, чтобы вызвать у детей интерес. Ведь развлекательный момент ознакомления с различными формами значительно облегчает весь следующий образовательный процесс. Вместе с этим дети учатся заострять внимание только на необходимом и проявлять самостоятельность.
Хронология обучения дошкольников простой начертательной геометрии будет следующей:
- изображенные на плотной бумаге разные фигуры, отличающиеся по цвету и размеру, называют и проговаривают вместе с ребенком;
- обведение очертаний фигур на картоне и последующее их разукрашивание определенными цветами, сравнение размеров изображений;
- вырезанные фигуры располагают по разным местам дома, чтобы дети потом их находили и называли, проговаривая также размер и цвет;
- предложение поиграть с разными мозаиками и пирамидками из геометрических фигур;
- отождествление с другими предметами в окружающей среде.
Способов изучения геометрических фигур предостаточно, среди них выделяются:
- наблюдающий, когда детей знакомят с вырезанными из картона образцами форм, а потом спрашивают о них;
- сравнительный, при котором дошкольники рассматривают парные карточки с фигурами и отмечают их отличия и схожесть;
- закрепительный, заключающийся в опросе детей о пройденном материале.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Что такое луч?
Каждый лучик имеет начало, продолжается бесконечно, как одноименная фигура.
Луч – это часть прямой, ограниченная начальной точкой с одной стороны. Лучи обозначают заглавными и строчными буквами латиницы.
Точкой А прямая поделена на два луча: луч А, луч АС (в начале ставится символ начала луча).
Для рассмотрения следующего понятия, вспомним мультфильм «38 попугаев». Серию, где друзья пытались измерить удава. Если рассматривать удава с математической точки зрения, тов математике его бы обозначили, отрезком.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
к оглавлению ^
Из бумаги
Из картона
Развертки куба
к оглавлению ^
Треугольника
к оглавлению ^
Прямоугольника
к оглавлению ^
Цилиндра
Ромба
Призмы
к оглавлению ^
Задание 2 (построение прямоугольного треугольника)
Постройте на нелинованной бумаге треугольник , чтобы угол был прямым, длина стороны равнялась 15 см, а длина сторогы – 20 см.
Построим точку (Рис. 18).
Рис. 18. Точка
Проведем через точку прямую (Рис. 19).
Рис. 19. Прямая, проведенная через точку
Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон совпала с лучом, как показано на рис. 20.
Рис. 20. Построение прямого угла
Проведем по второй стороне прямого угла треугольника луч из точки и получим прямой угол (Рис. 21).
Рис. 21. Полученный прямой угол
Выполним построение сторон треугольника. Построим отрезок , который равен 15 см (Рис. 22).
Рис. 22. Отрезок
Построим отрезок , который равен 20 см (Рис. 23).
Рис. 23. Отрезок
Соединим полученные точки отрезком . Мы получили прямоугольный треугольник (Рис. 24) с прямым углом и сторонами см и см.
Рис. 24. Треугольник
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
к оглавлению ^
Конуса
к оглавлению ^
Пирамиды
к оглавлению ^
Шестигранника
к оглавлению ^
Макета с припусками
Параллелепипеда
к оглавлению ^
Трапеции
к оглавлению ^
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
к оглавлению ^
Многогранника
к оглавлению ^
Параллелограмма
Задание 1 (определение вида треугольников)
Назовите номера тупоугольных, остроугольных и прямоугольных треугольников на рисунке 16.
Рис. 16. Иллюстрация к заданию 1
Треугольник номер 1 – остроугольный, у него все углы острые. Треугольники номер 3 и 4 – тупоугольные, каждый из них имеет один тупой угол. Фигура номер 2 – прямоугольный треугольник. Проверим, действительно ли эта фигура имеет прямой угол, с помощью прямоугольного треугольника (Рис. 17).
Рис. 17. Проверка треугольника номер 2
Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
к оглавлению ^
Сложных фигур
3d
Октаэдра
к оглавлению ^
Тетраэдра
к оглавлению ^
Икосаэдра
к оглавлению ^
Додекаэдра
к оглавлению ^
Гексаэдра
Фигурок из треугольников
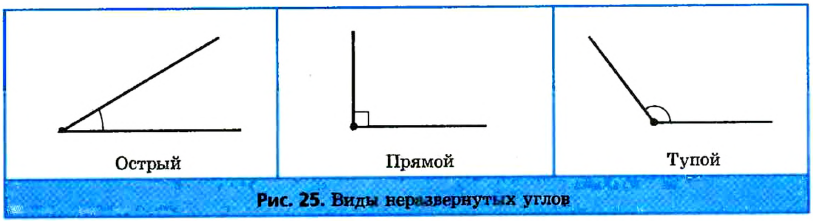
Виды углов
Развернутый угол. (Рис. 4)
Угол называется развернутым, если его стороны лежат на одной прямой.
Рис. 4. Виды углов: развернутый
Прямой угол (Рис. 5)
Прямой угол составляет половину развернутого.
Рис. 5. Виды углов: прямой угол
Прямой угол можно получить путем складывания бумаги. Сложив лист дважды, мы получим модель прямого угла, его составляют линии сгиба.
Приложим модель угла к углу на чертеже (Рис. 5) таким образом, чтобы углы и стороны совпали (Рис. 6).
| Рис. 5. Модель угла и угол на чертеже | Рис. 6. Модель угла, приложенная к углу на чертеже |
Мы убедились, что на чертеже действительно изображен прямой угол.
Для удобства определения, прямой угол или нет, используют особый инструмент – прямоугольный треугольник (Рис. 7).
Рис. 7. Прямоугольный треугольник
Непрямые углы делятся на острые (Рис. 
| Рис. 8. Виды углов: острый угол Острый угол меньше прямого (Рис. 10). Рис. 10. Сравнение острого и прямого угла |
Рис. 11. Виды углов: тупой угол
Тупой угол больше прямого (Рис. 12). Рис. 12. Сравнение тупого и прямого угла |
Макеты из бумаги
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
к оглавлению ^
Оригами
Дом
к оглавлению ^
Животные
Корабль
Применяется множество вариантов, как сделать кораблик из бумаги.
Простая схема.
Полигональные чертежи
Игрушки из фигур
Геометрические маски
к оглавлению ^
Карандаш
( 1 оценка, среднее 5 из 5 )
Содержание:
Геометрия — наука о геометрических фигурах и их свойствах. Самая простая геометрическая фигура — точка. Каждая другая геометрическая фигура состоит из точек, то есть является некоторым множеством точек. Другие фигуры — прямая, плоскость. Их содержание раскрывают не определениями, а описывая их основные свойства. Фигуры, расположенные на одной плоскости, называют плоскими. Раздел геометрии, в котором изучаются фигуры на одной плоскости, называется планиметрией.
Мы начинаем изучать планиметрию — раздел геометрии, в котором рассматриваются фигуры на плоскости. Из курса математики вы уже имеете представление о некоторых из них. Наша ближайшая цель — восстановить и дополнить эти начальные знания. Геометрические сведения мы будем излагать в определенной логической последовательности, чтобы они стали прочным фундаментом для дальнейшего изучения геометрии.
Основу любой науки составляют утверждения, которые принимаются как исходные и не требуют обоснования. В математике такие утверждения называют аксиомами. Аксиомы планиметрии, которые мы рассмотрим в этой главе, выражают основные свойства простейших геометрических фигур. На их основе с помощью логических рассуждений мы будем получать более сложные геометрические факты.
Планиметрия — от латинского «планум» и греческого «метрио» — измеряю.
Определения
Основные свойства расположения точек на прямой:
- Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.
- Через любые две точки можно провести прямую, и только одну.
- Из трех точек прямой одна и только одна лежит между двумя другими.
Части прямой — отрезок и луч. Отрезок АВ — это часть прямой, содержащая точки А, В и все точки, лежащие между ними. Каждому отрезку соответствует его длина. Длина отрезка — расстояние между его концами. Расстояние и длину измеряют метрами, сантиметрами, миллиметрами, километрами, футами, дюймами и другими единичными отрезками.
Основные свойства измерения отрезков:
Каждый отрезок имеет определенную длину.
Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Часть плоскости, ограниченная двумя лучами с общим началом, называется углом. Углы бывают острые, прямые, тупые, развернутые и больше развернутого. Меры углов определяют в градусах, минутах, секундах, румбах и некоторых других единицах измерения.
Основные свойства измерения углов:
Каждый угол имеет определенную меру.
Мера угла равна сумме мер углов, на которые данный угол делится его внутренним лучом.
Биссектриса угла — внутренний луч, разбивающий данный угол на два равных угла.
Точки и прямые
Геометрия — это наука о геометрических фигурах и их свойствах. Самая простая геометрическая фигура — точка. Любая другая геометрическая фигура состоит из точек. Например, окружность — это фигура, состоящая из всех точек плоскости, равноудаленных от данной точки (рис. 1).
Отрезок также состоит из точек. Любое множество точек является геометрической фигурой. Часть геометрической фигуры или объединение нескольких фигур — тоже геометрическая фигура (рис. 2).
Одна из геометрических фигур — плоскость. Представление о части плоскости дает поверхность стола, потолка, пола. В геометрии плоскость считается неограниченной, идеально ровной и гладкой.
Фигуры, расположенные на одной плоскости, называют плоскими. Все вышеназванные геометрические фигуры — плоские. А куб, шар, прямоугольный параллелепипед — неплоские фигуры (рис. 3). Раздел геометрии, в котором изучаются фигуры на одной плоскости, называется планиметрией (латинское planum — плоскость).
Мы начинаем изучать планиметрию. Прежде всего рассмотрим, как могут быть расположены на плоскости точки и прямые.
Вы уже знаете, как с помощью линейки проводят прямые (рис. 4).
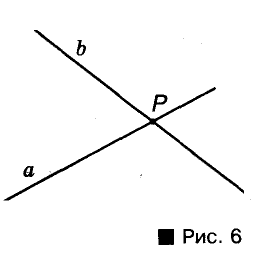
Прямая в геометрии — идеально ровная и бесконечная в обе стороны. Кик и любая другая фигура, прямая состоит из точек. Если точка А лежит на прямой а, говорят, что прямая а проходит через точку А. Записывают так: А е а. Если точка В не лежит на прямой а, пишут: 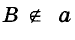
Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.
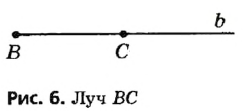
Через одну точку можно провести много прямых. На рисунке 6 вы видите прямые а и Ь, проходящие через точку Р. Это их общая точка, других общих точек прямые а и Ъ не имеют. Если две прямые имеют только одну общую точку, говорят, что они пересекаются в этой точке. Прямые а и b Пересекаются в точке Р.
Если прямой принадлежат точки А и В, говорят, что эта прямая проходит через точки А и В. Обозначают ее так: АВ.
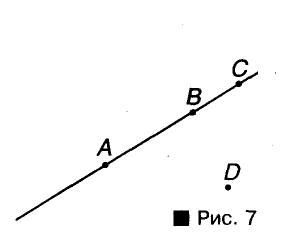
Через любые две точки можно провести прямую, и только одну.
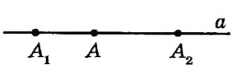
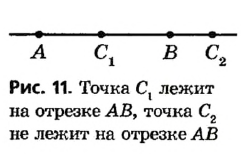
Можно ли провести прямую через три точки? Не всегда. Если точки А, B и C расположены, как показано на риcунке 7, через них прямую провести можно. А через точки А, В и D — нельзя. Говорят, что точки А, В и D Не лежат на одной прямой. Точки А, В, (- лежат на одной прямой, причем В — между А и С.
Простейшие геометрические фигуры и их свойства
Из трех точек прямой одна и только одна лежит между двумя другими.
Если точка В лежит между А и С, говорят, что точки А и С лежат по разные стороны от В, а точки А и В — по одну сторону от С.
Напечатанные выше жирным шрифтом три предложения со значком 
Любая точка А прямой делит эту прямую на две части (рис. 8). Каждую из частей прямой вместе с точкой А называют лучом, выходящим из точки А. Точку А называют началом луча. Если говорят «луч АВ», то имеют в виду, что начало луча находится в точке А (рис. 9).
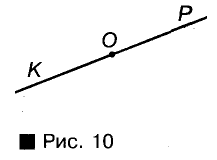
Два луча, имеющие общее начало и дополняющие друг друга до прямой, называются дополнительными. На рисунке 10 вы видите луч ОК — дополнительный для луча ОР и луч ОР — дополнительный для ОК.
Геометрия — часть математики (рис. 11). Геометрическая наука богата содержанием и методами исследования. Она включает элементарную геометрию, высшую геометрию, неевклидовы геометрии, топологию и др. В школе изучают только элементарную геометрию.
Геометрия тесно связана со многими другими науками, прежде всего с физикой. Но физика занимается изучением материальных тел (имеющих массу, температуру, цвет и т. п.), а в геометрии абстрагируются от всего материального. Абстрагироваться — означает мысленно отвлечься от конкретных объектов, окружающих нас. Абстрагируясь от материальных вещей, мы в воображении создаем идеальные объекты по сходным свойствам. Конец иголки, натянутая струна — это материальные объекты. Они имеют определенную толщину, длину, массу. Абстрагируясь от таких физических свойств, человеческое воображение создало абстрактные геометрические понятия точка, прямая. В природе абстрактной прямой нет, но это понятие существует в человеческом воображении. И очень полезное понятие, поскольку все свойства прямой и ее частей, выявленные в геометрии, переносятся на миллионы и миллиарды всех натянутых струн, прямолинейных рельсов, труб, лент и т. п. Не существует в природе и плоскость без толщины, идеально ровная и гладкая, бесконечная в каждом ее направлении. Но для науки это идеальное понятие очень важно, поскольку свойства, установленные в геометрии для плоскости и ее частей, можно переносить на свойства миллиардов конкретных стен, оконных стекол и других предметов, имеющих плоские поверхности.
Пример №1
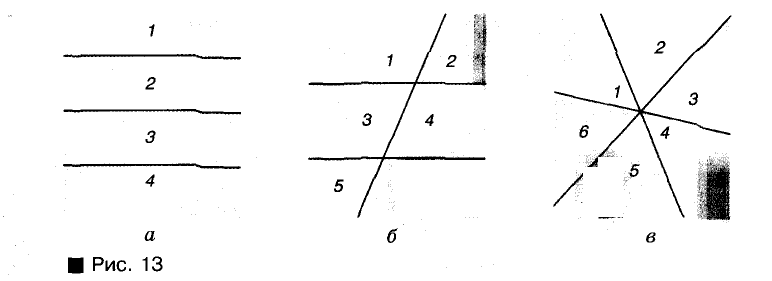
На сколько частей могут разбивать плоскость три ее прямые?
Решение:
Если прямые расположены, как показано на рисунке 12, то они разбивают плоскость на 7 частей. Если они расположены, как показано на рисунке 13, то они разбивают плоскость на «4 или 6 частей.
Ответ. Три прямые разбивают плоскость, которой они принадлежат, на 4, 6 или 7 частей.
Дополнительное объяснение точки и прямой:
Основными геометрическими фигурами на плоскости являются точка и прямая. Плоскость можно представить как лист бумаги, точку — как след, оставленный иголкой на этом листе, а прямую — как тонкую натянутую нить. Точки обычно обозначают прописными латинскими буквами (А, В, С, D, …), а прямые — строчными латинскими буквами (а, b, с, d, …).
Ha рисунке 1 точки А и D лежат на прямой 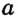
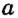
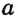
А и D, но не проходит через точки В и С.
Рис. 1
Прямая бесконечна и состоит из бесконечного множества точек. На рисунках мы изображаем лишь часть прямой.
Свойства точек и прямых
Через одну точку на плоскости можно провести бесконечно много прямых. Рассмотрим прямые 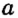
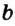
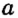
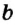
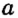
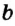
Рис. 2
Если на плоскости обозначены две точки [1] А и В, то через них можно провести прямую с (рис. 3). Отметим, что через точки А и B невозможно провести другую прямую, которая не совпадала бы с прямой с.
Это свойство называют аксиомой проведения прямой.
Рис. 3
[1] Здесь и далее, говоря «две точки» («две прямые», «три точки» и т. д.), мы будем считать, что эти точки (прямые) различны.
Аксиома проведения прямой
Через любые две точки можно провести прямую, и притом только одну.
Аксиома — от греческого «аксиос» — общепринятый, безоговорочный, не вызывающий сомнения
Из этого следует, что две прямые не могут иметь две или более общих точек: они либо имеют одну общую точку, либо не имеют общих точек вообще. Прямую, с выбранными на ней двумя точками, можно обозначать прописными буквами, которыми названы эти точки. Так, прямую на рисунке 3 можно назвать прямой АВ или прямой ВА.
Через три точки плоскости не всегда можно провести прямую. Так на рисунке 1 нельзя провести прямую через точки А, В, D.
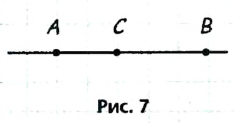
На рисунке 4 точки А, В, С лежат на одной прямой, причем точка С лежит между точками А и В. Можно также сказать, что точки А и В лежат по разные стороны от точки С.
Точки В и С лежат по одну сторону от точки А , а точки А и С лежат по одну сторону от точки В.
Аксиома расположения точек на прямой:
Из трех точек на прямой одна и только одна лежит между двумя другими.
Луч
Любая точка делит прямую на две части (рис. 5). Каждую из этих частей можно условно считать половиной прямой, поэтому образовавшиеся части прямой и получили название «полупрямые», или иначе — лучи
Рис. 5 Точка А делит прямую а на две полупрямые 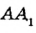
Лучом (или полупрямой) называется часть прямой, состоящая из всех Точек этой прямой, лежащих по одну сторону от некоторой данной на ней точки, а также самой этой точки. Данная точка называется начальной точкой (или началом) луча.
На рисунке 5 точка А — начальная точка двух лучей прямой 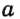
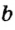
Два различных луча одной прямой с общей начальной точкой называются дополнительными лучами.
На рисунке 5 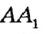
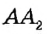
Пример №2
На прямой точка С лежит между точками А и В. Могут ли лучи АВ и АС быть дополнительными? Ответ обоснуйте.
Решение:
Пусть А, В и С — данные точки (рис. 7). Поскольку точка С лежит между точками А и В, то точки С и В лежат по одну сторону от точки А, значит, они принадлежат одному лучу с началом А. Этот луч можно назвать АВ или АС. Следовательно, данные лучи совпадают, поэтому они не являются дополнительными.
Ответ: не могут.
Отрезки и их длины
Две точки прямой делят эту прямую на три части: два луча и отрезок.
Отрезком АВ называется та часть прямой, которая состоит из точек А а В и всех точек, лежащих между ними. Точки А и В называют концами отрезка АВ. Все другие точки этого отрезка — его внутренние точки.
На рисунке 19 изображен отрезок АВ.
Точки А и В — его концы, а любая точка, лежащая между А и В, — внутренняя точка отрезка АВ.
Два отрезка пересекаются, если они имеют только одну общую внутреннюю точку.
Чтобы измерять отрезки, нужно иметь единичный отрезок (единицу измерения).
Отрезок, показанный на рисунке 20, будем считать единичным. Его длина равна 1 см.
Если на отрезке АВ единичный отрезок откладывается ровно 3 раза, то это значит, что длина отрезка АВ равна 3 см (рис. 21). Если на отрезке ЕР единичный отрезок откладывается два раза с остатком, а в остатке десятая часть единичного отрезка — 7 раз, то длина отрезка ЕР равна 2,7 см. Записывают так: АВ = 3 см, ЕР = 2,7 см.
За единичный отрезок можно брать отрезки длиной 1 м, 1 км, I фут, 1 дюйм и т. д.
Каждый отрезок имеет определенную длину.
Два отрезка называются равными, если длины их равны. Из двух отрезков большим считается тот, длина которого больше.
В сантиметрах измеряют сравнительно небольшие отрезки. Большие отрезки измеряют в дециметрах, метрах, километрах; меньшие — в миллиметрах. Напомним, что
1 км = 1000 м, 1 м = 10 дм = 100 см = 1000 мм.
Длину отрезка называют также расстоянием между его концами. Если ХУ = 18 см, то это означает, что расстояние между точками X и У равно 18 см. Расстояние между X и У всегда равно расстоянию между У и X.
Если точка С отрезка АВ разбивает его на две части, длины которых равны, например 2 см и 1,2 см, то длина отрезка АВ равна 3,2 см (рис. 22).
Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Напечатанные выше жирным шрифтом два предложения со значком 
Серединой отрезка называется его внутренняя точка, разбивающая этот отрезок на две равные части.
Если точка С — середина отрезка АВ, то АС = СВ (рис. 23).
Если точка С не принадлежит отрезку АВ, то сумма длин отрезков АС и СВ больше длины АВ. Таким образом, для любых трех точек А, В и С всегда АВ + ВС > АС.
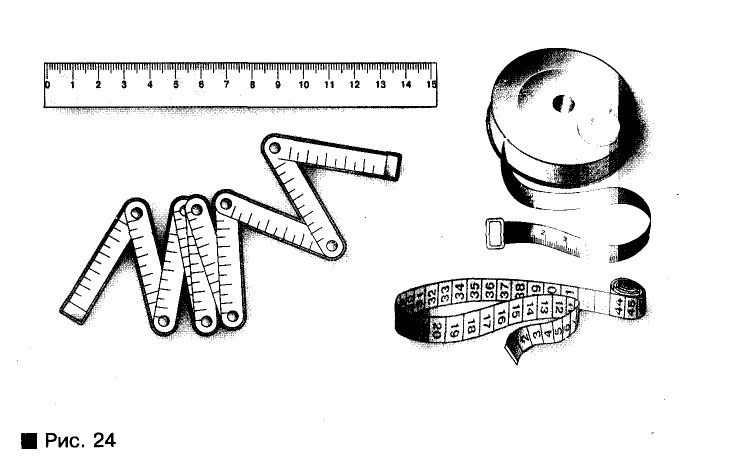
Измерять длины отрезков приходится многим специалистам. Чертежники измеряют их масштабными линейками, столяры — складными метрами, портные — клеенчатыми сантиметрами, строители — рулетками (рис. 24).
Для любознательных:
Измерительные приборы обеспечивают ту или иную точность. Расстояние между городами обычно определяют с точностью до километра, между берегами реки — с точностью до метра, длину карандаша — с точностью до миллиметра, диаметр детали ручных часов — с точностью до десятой, а то и сотой части миллиметра. Разумеется, для измерений разных длин и расстояний используют соответствующие измерительные приборы: кроме уже названных, циркули, кронциркули, штангенциркули, дальномеры и др. С некоторыми из них вы познакомитесь позже. Единицы длины бывают разные. В англоязычных странах чаще всего используют следующие: фут, дюйм, миля. Подробнее о них — дальше.
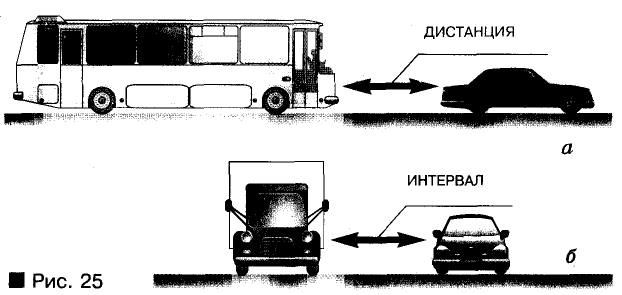
На практике для различных расстояний существуют разные названия: длина, ширина, высота, глубина, дистанция, интервал (рис. 25).
Пример №3
Луч — часть прямой. Можно ли утверждать, что луч короче прямой?
Решение:
Прямая и луч не имеют длины, поэтому сравнивать и длины нет смысла.
Ответ. Нет.
Пример №4
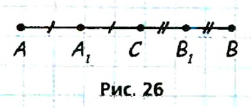
Точки К, Р и Т лежат на одной прямой. Найдите расстояние между Р и Т, если КР ~ 1,7 м, КТ = 4,8 м. Сколько решений имеет задача?
Решение:
Отметим точки К и Т так, что КТ = 4,8 м. Точка Р пр* мой КТ находится на расстоянии 1,7 м от К. Возможно два случая (рис. 26):
а) К лежит между PvlT: РТ = 1,7 м + 4,8 м = 6,5 м;
б) Р лежит между К и Т: РТ = 4,8 м — 1,7 м = 3,1 м.
Ответ. Задача имеет два решения: 6,5 м; 3,1 м.
Углы и их меры
Два луча, имеющих общее начало, разделяют плоскость на две части.
Часть плоскости, ограниченная двумя лучами с общим началом, называется углом.
Лучи, ограничивающие угол, называются сторонами, а их общее начало — вершиной уела (рис. 30, а). Такой угол называют углом А О В, или углом В О А, или углом О и записывают соответственно: 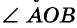
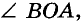
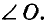
Угол, стороны которого — дополнительные лучи, называют развернутым углом (рис. 31).
Чтобы измерять углы, необходимо иметь единицу измерения. Такой единицей принято считать угол в 1 градус (сокращенно: 1°).
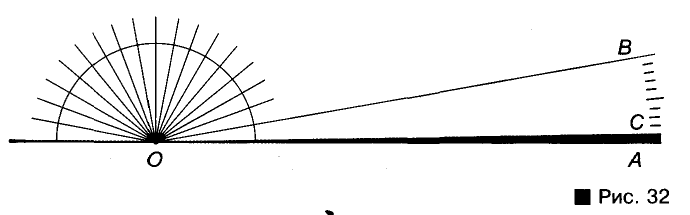
В развернутом угле он вмещается 180 раз.
Представим полуокружность, разделенную на 18 равных дуг (рис. 32). Если из ее центра О через все точки деления и концы полуокружности провести лучи, они разделят развернутый угол на 18 углов по 10°. Один из таких углов (АОВ) делим на 10°. Мера угла АОС равна 1°.
Каждый угол имеет определенную меру.
Мера развернутого угла равна 180°.
Меру угла обозначают так же, как и угол. Например, если мера угла ABC равна 60 градусам, пишут: 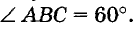
Минутой называют 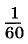
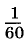
Записывают так: 1° = 60′, 1′ = 60″.
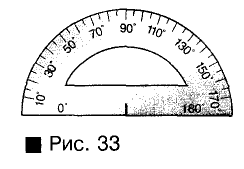
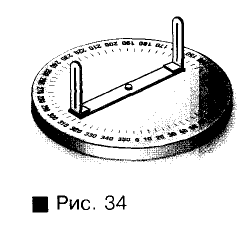
Углы в тетради и на классной доске измеряют транспортиром (рис. 33), а на местности — астролябией (рис. 34), теодолитом (рис. 35) или другими угломерными приборами.
Два угла называются равными, если их меры равны.
Из двух углов большим считается тот, мера которого больше.
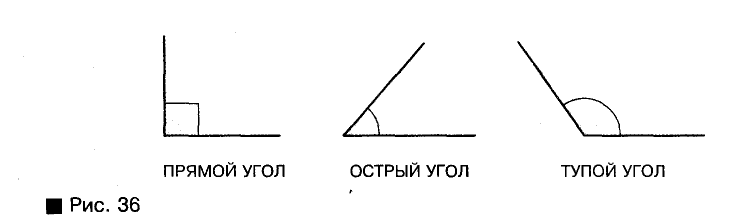
Угол называется прямым, если его мера равна 90°, острым — если он меньше прямого, тупым — если он больше прямого, но меньше развернутого (рис. 36).
Прямые углы на рисунках чаще обозначают не дугами, а квадратиками.
Углы больше развернутого (см. рис. 30, в) пока рассматривать не будем.
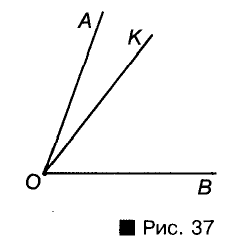
Луч, который исходит из вершины угла и лежит в его внутренней области,
называют внутренним лучом угла.
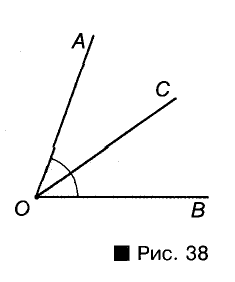
Внутренний луч делит данный угол на дна меньших угла. Например, внутренний луч ОК угла АОВ делит этот угол на углы АОК и КОВ (рис. 37). При этом 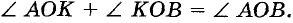
Мера угла равна сумме мер углов, на которые данный угол делится его внутренним лучом.
Два выделенных выше предложения со значком в — это основные свойства измерения углов.
Внутренний луч, который делит угол на два равных угла, называется биссектрисой этого угла. На рисунке 38 луч
ОС — биссектриса угла АОВ.
Для любознательных:
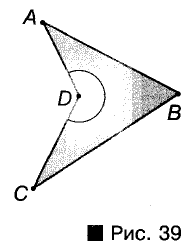
Углом часто называют также фигуру, составленную из двух лучей, имеющих общее начало, то есть углом называют и некую линию. Но разделить подобный угол на два или более равных углов нельзя. Таким образом, когда говорят о сложении, вычитании или делении углов, то угол рассматривают вместе с его внутренней областью. И хотя далее мы будем рассматривать в основном углы меньше развернутого, необходимо помнить, что бывают углы и больше развернутого, то есть больше 180°. Таким, например, является угол D четырехугольника ABCD (рис. 39).
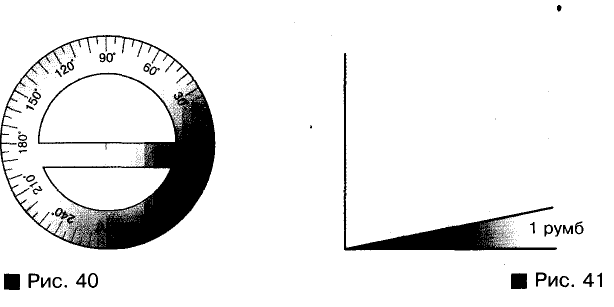
Существуют и специальные транспортиры, которыми измеряют углы больше развернутого (рис. 40). Понятие угла часто используют также для характеристики поворотов. Например, велосипедное колесо можно повернуть на 100°, можно на 300°. А если колесо сделало полтора оборота? Считают, что оно повернулось на 360° и еще на 180°, всего — на 540°.
Кроме градусов, минут и секунд, существуют и другие меры углов. Моряки измеряют углы в румбах. Румбом называют одну восьмую часть прямого угла, 1 румб = 11,25° (рис. 41). Научные работники чаще всего измеряют углы в радианах. Что это такое, вы узнаете в старших классах.
Пример №5
Найдите меру угла А О В, если лучи ОС и О К делят его на три равных угла и 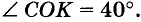
Решение:
Угол СОК — третья часть угла АО В. Поэтому 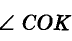
Ответ. 120°.
Пример №6
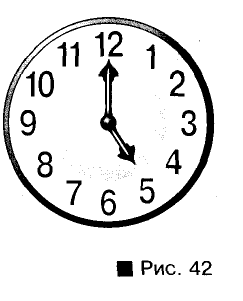
Найдите меры углов, образованных стрелками часов: в 3 часа; в 5 часов (рис. 42).
Решение:
На циферблате часов полуокружность соответствует 6 часам. Поэтому одному часу соответствует 1/6 часть развернутого угла, то есть 30°. Когда часы показывают 3 часа, угол между часовой и минутной стрелками равен 30° • 3 =
= 90°. Когда часы показывают 5 часов, угол между стрелками равен 30° 5 = 150°.
Ответ. 90°; 150°.
Определение и его роль в геометрии
В пункте 1.3 описаны два понятия — «луч», которое известно вам из курса математики 5 класса, и новое понятие — «дополнительные лучи». Благодаря этим описаниям можно четко представить, какие именно фигуры рассматриваются. Данные нами описания являются определениями, указывающими на особенности описанной фигуры, которые отличают ее от других фигур.
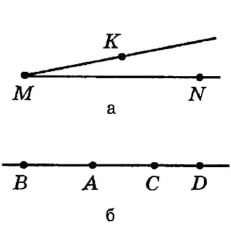
Прочитаем еще раз определение дополнительных лучей. Если в нем пропустить лишь слова «одной прямой», то лучи MN и МК на рисунке 8, а придется считать дополнительными. Если же не уточнить, что дополнительные лучи должны иметь общее начало, то лучи АВ и CD на рисунке 8, б тоже следует назвать дополнительными. Таким образом, эти измененные определения не будут описывать тот объект, который мы имеем в виду.
Рис. 8. К объяснению понятия «дополнительные лучи»:
а) лучи MN и МК не дополнительные;
б) лучи АВ и CD не дополнительные
Эти соображения свидетельствуют о том, как важно уделять внимание каждому слову в определении: только так можно по-настоящему понять геометрию.
Отрезок. Измерение и откладывание отрезков
Определение отрезка
Любой луч является частью прямой, «ограниченной» с одной стороны начальной точкой. Рассмотрим теперь отрезок — часть прямой, «ограниченную» точками с обеих сторон. Определение Отрезком называется часть прямой, состоящая из двух данных точек этой прямой (концов отрезка) и всех точек, лежащих между ними. Отрезок обозначают, записывая его концы в произвольном порядке. Так, отрезок на рисунке 10 можно назвать «отрезок АВ » или «отрезок ВА». Очевидно, что отрезок АВ является частью прямой АВ. При этом следует различать, идет ли речь о прямой АВ или об отрезке АВ.
Если рассмотреть вместе с точками А и В некоторую другую точку прямой, то, в соответствии с аксиомой расположения точек на прямой, она либо лежит между точками А и В , то есть принадлежит отрезку АВ (на рисунке 11 такой точкой является 
Равенство отрезков. Середина отрезка
Определение:
Два отрезка называются: равными, если они совмещаются наложением.
Нанесем отрезок 
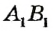
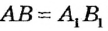
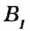
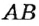
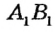
Определение:
Серединой отрезка называется точка отрезка, делящая его пополам (то есть на два равных отрезка).
На рисунке 14 отрезки DE и EF равны, то есть точка Е — середина отрезка DF. Обычно на рисунках равные отрезки обозначают одинаковым количеством черточек.
Измерение и откладывание отрезков
Важным свойством отрезка является его длина. Она выражается положительным числом, которое может быть определено сравнением данного отрезка с отрезком, принятым за единицу измерения,— единичным отрезком. В качестве единичного отрезка можно выбрать отрезок любой длины. На практике выбирают единичные отрезки длиной 1 мм, 1 см, 1 м и др.
Например, на измерительной линейке, которой мы обычно пользуемся, маленькие деления задают единичные отрезки длиной 1 миллиметр, а большие — длиной 1 сантиметр (рис. 15).
Прикладывая линейку к данному отрезку, мы определяем, сколько единичных отрезков и их частей в нем содержится. Это число выражает длину отрезка. Число, выражающее длину отрезка, зависит от единицы измерения.
На рисунке 15 длина отрезка СЕ равна 70 мм, или 7 см, или 0,07 м и т. д. Длина отрезка CD равна 3 см, а отрезка DE — 4 см. Можно сказать, что отрезок СЕ состоит из двух частей — отрезков CD и DE . Точка D лежит между точками С и Е, а длина отрезка СЕ равна сумме длин отрезков CD и DE (пишут так: CD + DE = СЕ ).
Сформулируем аксиомы измерения и откладывания отрезков.
Аксиома измерения отрезков
Каждый отрезок имеет определенную длину, которая выражается положительным числом в заданных единицах измерения. Длина отрезка равна сумме длин частей, на которые отрезок делится любой его точкой.
Аксиома откладывания отрезков
Hа любом луче от его начальной точки можно отложить отрезок данной длины и только один.
Очевидно, что измерение отрезков состоит в последовательном наложении на данный отрезок определенного количества единичных отрезков. Поэтому равные отрезки имеют равные длины, а больший отрезок имеет большую длину. Верно и другое утверждение: если отрезки имеют равные длины, то они равны, а большим из двух отрезков является тот, который имеет большую длину. Таким образом, для сравнения отрезков можно сравнить их длины.
Длину отрезка АВ называют также расстоянием между точка ми А и В. Часто, говоря «отрезок AB », мы имеем в виду его длину.
Пример №7
На луче АВ отмечена точка С, причем АВ = 12см, ВС — 7 см. Найдите длину отрезка АС
Решение:
Рассмотрим два случая расположения точки С на луче АВ.
- Точка С не лежит на: отрезке АВ (рис. 16, а). Тогда точка В лежит на отрезке АС По аксиоме измерения отрезков АС = АВ + ВС, то есть АС = 12 +7 =19 (см).
- Точка С лежит на отрезке АВ (рис. 16, 6). Тогда АВ = АС + ВС, то есть 12= АС + 7. Таким образом, АС = 12 — 7 = 5 (см).
Ответ: 19 см или 5 см.
Измерение, откладывание и определение углов
При изучении дополнительных лучей мы рассматривали случай, когда два луча имеют общую начальную точку. Рассмотрим теперь случай, когда два луча имеют общую начальную точку, но не обязательно являются полупрямыми одной прямой.
Определение:
Углом называется геометрическая фигура, которая состоит из двух лучей (сторон угла), исходящих из одной точки (вершины угла).
Для обозначения углов используют знак 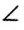
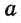
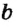
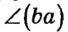
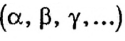
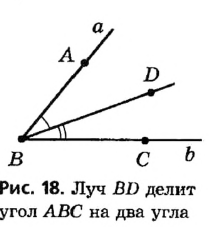
Стороны угла делят плоскость на две части. Внутренней областью угла считается та из них, которая целиком содержит любой отрезок с концами на сторонах угла (на рисунке 17, а она заштрихована). Луч, который исходит из вершины угла и проходит в его внутренней области, делит данный угол на два угла. На рисунке 18 луч BD делит угол ABC на углы ABD и DBC .
Определение:
Развернутым углом называется угол, стороны которого являются дополнительными лучами.
На рисунке 19 изображен развернутый угол АОВ.
Прямая АВ делит плоскость на две части, каждую из которых можно считать внутренней областью развернутого угла АОВ . Договоримся ту из частей, которую мы рассматриваем как внутреннюю, обозначать дужкой.
Равенство углов. Биссектриса угла
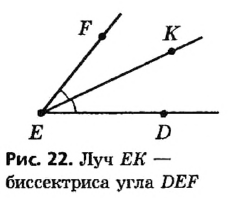
Определение:
Два угла называются равными, если они совмещаются наложением.
Биссектриса — от латинского «бис» — дважды и «секто» — рассекающая пополам.
На рисунке 20 изображены углы 1 и 2. Наложим угол 1 на угол 2 так, чтобы их вершины совпали, сторона первого угла совместилась со стороной второго, а внутренние области этих углов были расположены по одну сторону от прямой, содержащей совместившиеся стороны. Если другие стороны этих углов тоже совместятся, то углы 1 и 2 являются равными (пишут так: 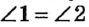
Если же эти стороны не совместятся, то меньшим считается тот угол, сторона которого принадлежит внутренней области второго угла. На рисунке 21 угол 1 является частью угла 2, то есть он меньше угла 2 (пишут так: 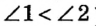
Определение
Биссектрисой угла называется луч, который исходит из вершины угла и делит угол пополам (то есть на два равных угла).
На рисунке 22 углы DEK и KEF равны, поэтому луч ЕК — биссектриса угла DEF . Обычно на рисунках равные углы обозначают одинаковым количеством дужек.
Измерение и откладывание углов
Измерение углов имеет много общего с измерением отрезков. Величина отрезка количественно выражается мерой (длиной) отрезка, а величина угла — мерой угла. Мера угла выражается положительным числом, которое можно определить измерением, основанным на сравнении данного угла с углом, принятым за единицу измерения.
Обычно такой единицей является 1 гра дус (обозначается 1°) — угол, равный 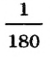
Градус — от латинского «градус» — шаг. По наблюдению вавилонян солнечный диск на дневном пути «делает 180 шагов».
Сформулируем аксиомы измерения и откладывания углов.
Аксиома измерения углов
Каждый угол имеет градусную меру. Которая выражается положительным числом. Развернутый угол равен 180°.
Если луч делит Данный угол на два угла, то градусная мера данного угла равна сумме градусных мер двух полученных углов;
Аксиома откладывания углов
От любого луча данной прямой можно отложить в заданную сторону от прямой угол с заданной градусной мерой, меньшей 180°, и только один.
Так, на рисунке 18 градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (это утверждение можно записать в виде равенства: 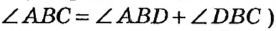
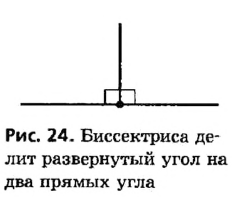
Биссектриса развернутого угла делит его на два угла, каждый из которых равен 90° (рис. 24). Такие углы называются прямыми. В отличие от других углов, обычно обозначаемых дужками, прямой угол обозначают знаком 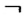
В 7 классе мы будем рассматривать углы, градусная мера которых не превышает 180°. Для более точных измерений используется 1 минута (обозначается 
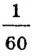
Неразвернутые углы делятся на три вида (рис. 25):
- острые углы, меньше 90°;
- прямые углы, равны 90°;
- тупые углы, больше 90°, но меньше 180°.
На практике для построения углов используют транспортир. Для построения прямых углов используют угольник.
Измерение углов можно считать последовательным наложением на данный угол определенного (не обязательно целого) числа углов, равных 1°. Поэтому равные углы имеют равные градусные меры, а больший угол имеет большую градусную меру. Верно и другое утверждение: если углы имеют равные градусные меры, то они равны, а из двух углов большим является тот, который имеет большую градусную меру. Таким образом, для сравнения двух углов достаточно сравнить их градусные меры.
Пример №8
Луч b делит угол (aс), равный 120° на два угла, один, из которых втрое меньше угла (ас) .
Найдите эти углы.
Решение:
Пусть угол ( ab) втрое меньше угла (ас). Тогда 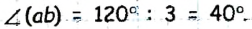
Тогда
Ответ:
Аналогия в геометрии
Иногда при решении задач о свойствах отрезков и углов применяются одни и те же методы и подходы. Это объясняется сходством некоторых свойств этих фигур. Такое сходство в науке называется аналогией.
Объясним суть аналогии на примере двух следующих задач.
Задача 1
На отрезке АВ, равном 20 см, отмечена точка С. Найдите расстояние между серединами отрезков АС и СВ.
Задача 2
Луч С делит угол (аb), равный 140°, на два угла. Найдите угол между биссектрисами углов (ас) и (ab).
На первый взгляд, перед нами совершенно разные задачи, поскольку в одной речь идет об отрезках, а во второй — об углах. Однако в обеих задачах дано некоторое «целое», разделенное на части. Кроме того, понятия середины отрезка и биссектрисы угла связаны с делением целого пополам, и в обеих задачах нам необходимо найти сумму половин каждой из частей фигуры.
Решение 1
Пусть точка С принадлежит отрезку АВ, точки 
Найдем длину отрезка
Поскольку по условию задачи АВ = 20 см, имеем:
Ответ: 10 см
Решение 2
Пусть луч с делит угол (аb) на два угла, лучи 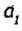
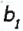
Тогда
Найдем градусную меру угла
Поскольку по условию задачи 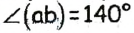
Ответ: 70°.
Как видим, в основе обоих решений лежит общая идея. Найдя ее при решении первой задачи, мы можем повторить основные этапы рассуждений применительно к условиям второй задачи, то есть решить ее аналогично.
Рассуждения по аналогии довольно часто применяются и в других науках. Например, биологи установили, что летучая мышь в полете испускает ультразвуковые колебания и, воспринимая колебания, отраженные от преграды, ориентируется по этим сигналам в темноте. По аналогичному принципу ученые создали радиолокатор, определяющий местонахождение объектов в любых погодных условиях. Но аналогия в науке не всегда дает желаемый результат: в течение многих веков человек старался взлететь в небо с помощью искусственных крыльев, аналогичных птичьим, но эти старания были напрасными. И только более основательные научные исследования привели к созданию дельтапланов, самолетов и других летательных аппаратов, с помощью которых человек поднялся в воздух. Выдающийся немецкий астроном и математик Иоганн Кеплер считал аналогии «своими верными учителями» и подчеркивал, что «аналогиями менее всего следует пренебрегать в геометрии». Однако при этом нужно учитывать, что аналогия, полезная как способ рассуждений, сама по себе не может служить доказательством каких-либо свойств геометрических фигур.
Определение параллельных прямых
Известно, что если две прямые на плоскости имеют только одну общую точку, то они пересекаются. Рассмотрим теперь случай, когда две прямые не имеют общих точек.
Параллельный — от греческого слова «параляелос» — идущий рядом
Определение:
Две прямые на плоскости называются параллельными, если они не пересекаются.
Представление о параллельных прямых дают, например, железнодорожные рельсы или линейки нотного стана.
На рисунке 29 прямые 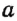
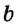
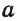
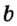
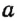
Итак, можно выделить два случая взаимного расположения прямых на плоскости: две прямые на плоскости или параллельны, или пересекаются.
Наряду с параллельностью прямых мы будем рассматривать также параллельность отрезков и лучей.
Определение:
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Аналогично формулируются определения параллельности двух лучей, прямой и отрезка, луча и отрезка и т. п.
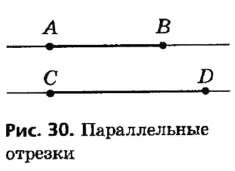
На рисунке 30 прямые АВ и CD параллельны, поэтому отрезки АВ и CD параллельны, лучи ВА и CD параллельны, отрезок АВ параллелен прямой CD и т. д.
На практике довольно часто приходится проводить прямую, параллельную данной,— например, делать разметку дороги или чертить поля в тетради. Всегда ли можно провести через данную точку прямую, параллельную данной? Сколько таких прямых проходит через точку, не лежащую на данной прямой? Ответ на эти вопросы дает аксиома параллельных прямых (аксиома Евклида).
Аксиома параллельных прямых (аксиома Евклида)
Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной1.
Мы сформулировали лишь некоторые из аксиом планиметрии. Более полный перечень аксиом представлен в Приложении 1.
Теорема о двух прямых, параллельных третьей
На основе аксиом с помощью логических рассуждений (доказательств) мы будем получать новые геометрические факты. В математике утверждение, справедливость которого устанавливается путем доказательства, называется теоремой.
Доказывая теорему, используют определения, ак сиомы и теоремы, доказанные ранее.
Итак, сформулируем и докажем первую теоре му — теорему о параллельных прямых (рис. 31).
Теорема: (о двух прямых, параллельных третьей)
Две прямые, параллельные третьей, параллельны между собой.
‘ На самом деле имеет место такое утверждение: «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну». Возможность провести такую прямую мы докажем в п. 14.3.
Доказательство:
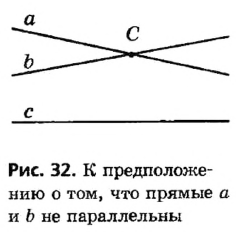
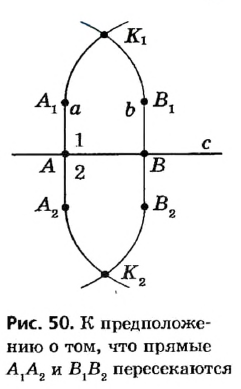
Пусть а, b и с — данные прямые, причем а || с, b || c. Докажем, что прямые а и b параллельны.
Предположим, что прямые а и b не параллельны. Тогда они должны пересекаться в некоторой точке С (рис. 32). Таким образом, через точку С проходят две прямые, параллельные прямой с. Но согласно аксиоме параллельных прямых через точку вне данной прямой может проходить не более одной прямой, параллельной данной. Следовательно, наше предположение о том, что прямые а и b могут пересекаться, неверно, то есть эти прямые параллельны. Теорема доказана.
Применим доказанную теорему для решения задачи.
Пример №9
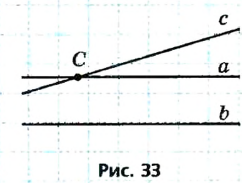
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую. Докажите.
Решение:
Пусть а || b, и прямая с пересекает прямую а (рис. 33). Докажем, что прямые b и с пересекаются. Предположим, что эти прямые не пересекаются. В таком случае b || с. Поскольку с || b и а || b, то по теореме о двух прямых, параллельных третьей, прямые а и с параллельны. Но это невозможно, так как по условию задачи прямые а и c пересекаются. Таким образом, предположение о том, что b || с, неверно. Значит, прямые b и с пересекаются, что и требовалось доказать.
Теорема — от греческого «теоремос» — рассматривать, обдумывать
Обратим внимание на рисунок 32, который использовался в ходе доказательства теоремы. Взаимное расположение прямых а, b, с на этом рисунке не соответствует формулировке теоремы, и это легко объяснить: ведь рисунок отражает предположение, впоследствии оказавшееся неверным. Вообще, рисункам в геометрических теоремах и задачах отводится особая роль — то, что на них изображено, следует из имеющихся у нас сведений, но не наоборот. Недоказанные свойства геометрических фигур, даже если они кажутся очевидными из рисунков, использовать нельзя. Рисунок в геометрии лишь отражает свойства и утверждения, выраженные словами, но сам по себе не является доказательством. К тому же рисунок может не охватывать всех возможных вариантов расположения элементов фигур, которые подразумеваются в задаче или теореме. Недаром геометрию называют «искусством правильно рассуждать на неправильных чертежах».
Условие и заключение теоремы. Доказательство от противного.
В формулировке любой теоремы всегда можно четко выделить две части: то, что дано (условие), и то, что надо доказать (заключение). Переформулируем теорему о двух прямых, параллельных третьей, следующим образом: «Если две прямые параллельны третьей прямой, то эти прямые параллельны между собой». Нам известно, что две прямые параллельны третьей прямой — это условие теоремы. Требуется доказать, что эти прямые параллельны между собой — это заключение теоремы. Вообще говоря, выделить условие и заключение легче всего для утверждения, представленного в виде: «Если… (условие), то… (заключение)».
Проанализируем доказательство теоремы о двух прямых, параллельных третьей. Сначала мы предположили, что прямые а и b не параллельны, то есть что заключение теоремы ошибочно. Затем, опираясь на известные свойства взаимного расположения прямых, установили, что через некоторую точку С проходят две прямые, параллельные с, то есть пришли к противоречию с аксиомой параллельных прямых. На основании этого противоречия мы сделали вывод о том, что наше предположение было неверным, а значит, верным является утверждение теоремы. Этот метод доказательства называется доказательством от противного, им мы воспользовались и в задаче, которую рассматривали после теоремы. Но этот метод не единственный: уже в следующем параграфе мы будем применять и другие методы доказательств.
Метод доказательства от противного иногда используется как в других науках, так и в повседневной жизни. Например, врач, чтобы убедиться, что пациент не болен гриппом, может рассуждать так: «Допустим, что у больного грипп; тогда у него должны быть характерные симптомы: повышение температуры, головная боль и т. п. Но этих симптомов нет, то есть предположение о гриппе неверно. Значит, пациент не болен гриппом».
Схема доказательства от противного
| Утверждение: | Если А, то В |
| Доказательство: | |
|
1. Пусть A, но не B |
Предполагаем, что условие теоремы выполняется, а заключение — нет |
| 2.Рассуждения |
Проводим рассуждения, опираясь на аксиомы и ранее доказанные теоремы |
| 3.Противоречие |
Получаем новое утверждение, противоречащее либо данному условию, либо одной из аксиом, либо ранее доказанной теореме |
| 4. Тогда B |
Убеждаемся, что наше предположение ошибочно, т. е. данное утверждение является верным |
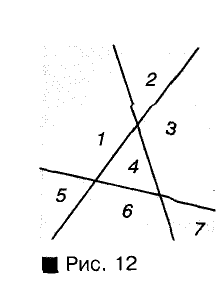
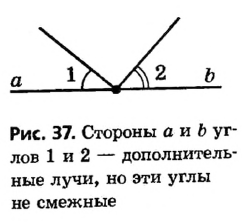
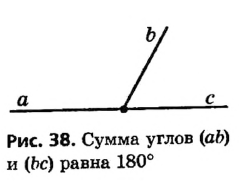
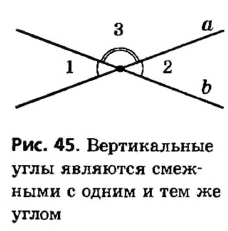
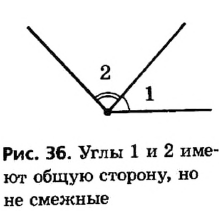
Определение смежных углов
В предыдущих параграфах мы рассматривали виды углов в зависимости от их градусной меры. Перейдем к изучению углов, имеющих общие элементы.
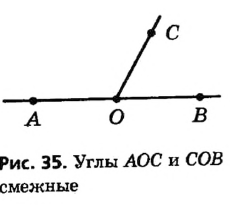
Пусть на прямой точка О лежит между точками А и В, а С — произвольная точка вне прямой АВ (рис. 35). Тогда углы АОС и СОВ имеют общую сторону, а стороны OA и ОВ данных углов являются дополнительными лучами.
Определение:
Два угла называются смежными, если они имеют общую сторону, а другие стороны этих углов являются дополнительными лучами.
Пропуск хотя бы одного условия в формулировании определения недопустим; это может привести к тому, что будет описан иной геометрический объект. Так, если стороны двух углов не являются дополнительными лучами, то даже при наличии общей стороны такие углы — не смежные (рис. 36). Не являются смежными и углы, которые не удовлетворяют первому условию определения, то есть не имеют общей стороны (рис. 37).
Теорема о смежных углах. Следствия из теоремы
Теорема (о смежных углах)
Сумма смежных углов равна 180° .
Доказательство:
Пусть углы ( аb ) и (bс) — данные смежные углы (рис. 38). Тогда по определению смежных углов лучи а и с дополнительные, то есть угол (ас) развернутый, а его градусная мера равна 180°. Луч b делит угол (ас) на два угла, и по аксиоме измерения углов 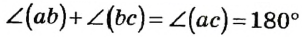
Сформулируем теперь несколько утверждений, которые легко обосновать с помощью доказанной теоремы.
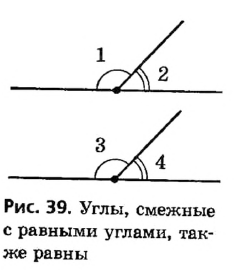
1. Если два угла равны, то смежные с ними углы также равны.
Действительно, по теореме о смежных углах 
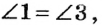
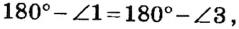
2. Два угла, смежные с одним и тем же углом, равны.
На рисунке 40 углы 1 и 2, а также углы 1 и 3 являются смежными. Поскольку сумма смежных углов равна 180°, то
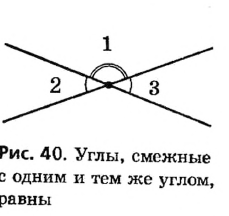
3. Угол, смежный с прямым углом, также прямой. Угол, смежный с тупым углом,— острый. Угол, смежный с острым углом,— тупой.
Эти утверждения вытекают из теоремы о смежных углах, поскольку 180°-90° = 90° (рис. 41), а если два неравных угла в сумме составляют 180°, то один из них больше 90° (то есть тупой), а второй — меньше 90° (то есть острый).
В математике утверждения, непосредственно вытекающие из теорем (или аксиом), называют следствиями. Обосновывая следствия 1—3, мы всякий раз упоминали теорему о смежных углах, причем делали это двумя способами: либо указывали ее название, либо пересказывали ее содержание. Такие обращения к известному утверждению с целью обоснования нового называют ссылками.
Решая геометрическую задачу или доказывая новую теорему, необходимо ссылаться на ранее изученные определения, аксиомы, теоремы и их следствия, а также на данные, содержащиеся в условии задачи или вытекающие из него. Например, при доказательстве теоремы о смежных углах мы ссылались на определения смежных углов, развернутого угла и аксиому измерения углов, а при доказательстве теоремы о двух прямых, параллельных третьей, — на аксиому параллельных прямых.
Пример №10
Докажите, что если два смежных угла равны, то они прямые.
Решение:
Если 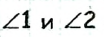
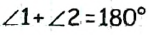
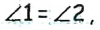
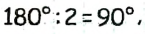
Вертикальные углы. Перпендикулярные прямые
Определение вертикальных углов
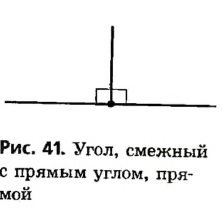
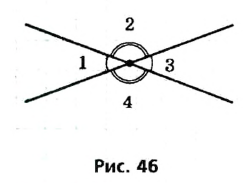
Рассмотрим еще один случай взаимного расположения углов с общими элементами. Вертикальный — от латинского «вертикалис» — вершинный
Определение:
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон второго. На рисунке 44 прямые АС и BD пересекаются в точке О. Стороны OD и OA угла AOD являются дополнительными лучами сторон ОВ и ОС угла ВОС , поэтому эти углы — вертикальные. Вертикальными являются также углы АОВ и DОС.
Таким образом, при пересечении двух прямых1 образуются две пары вертикальных углов. Наглядное представление о вертикальных углах дают, например, обычные ножницы.
Теорема о вертикальных углах. Угол между прямыми
Основное свойство вертикальных углов выражает следующая теорема.
Теорема: (о вертикальных углах )
Вертикальные углы равны.
1 Здесь и далее, говоря об углах, образованных при пересечении двух прямых, мы будем иметь в виду неразвернутые углы.
Доказательство:
Пусть 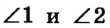
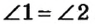
Пример №11
Сумма двух углов, образовавшихся при пересечении двух прямых, равна 100°. Найдите все образовавшиеся углы.
Решение:
По условию задачи при пересечении двух прямых образовались два угла, сумма которых составляет 100°. Эти углы могут быть или смежными, или вертикальными. Сумма смежных углов равна 180°, поэтому данные углы не могух быть смежными, значит, они вертикальные. Пусть 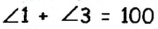
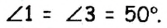
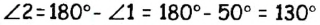
Поскольку углы 2 и 4 вертикальные, то 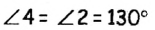
Ответ: 50°; 130°; 50°; 130°.
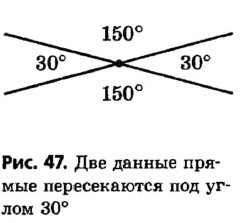
Определение:
Углом между двумя прямыми называется меньший из углов, образовавшихся при их пересечении.
На рисунке 47 две прямые при пересечении образуют два угла по 30° и два угла по 150°. Угол между данными прямыми по определению равен 30° (иначе говорят: прямые пересекаются под углом 30°).
Очевидно, что если при пересечении двух прямых образуются четыре равных угла, то все они равны 90°, то есть данные прямые пересекаются под прямым углом.
Перпендикулярные прямые
Перпендикулярный— от латинского слова «перпендикулярис» — отвесный.
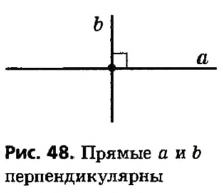
Определение:
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
На рисунке 48 прямые а и b перпендикулярны. Кратко это обозначают так: 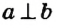
Отрезки или лучи называются перпендикулярными, если они лежат на перпендикулярных прямых.
Докажем важное утверждение; связывающее понятия перпендикулярности и параллельности прямых.
Теорема (о двух прямых, перпендикулярных третьей) Две прямые, перпендикулярные третьей, параллельны.
Утверждение теоремы иллюстрирует рисунок 49. На этом рисунке
Доказательство:
Пусть даны прямые 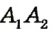
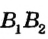
Предположим, что данные прямые не параллельны. Тогда они пересекаются в некоторой точке 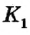
Перегнем рисунок по прямой АВ. Поскольку прямые углы 1 и 2 равны, то при перегибе луч 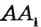
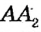
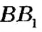
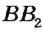
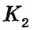
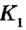
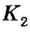
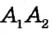
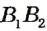
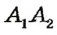
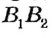
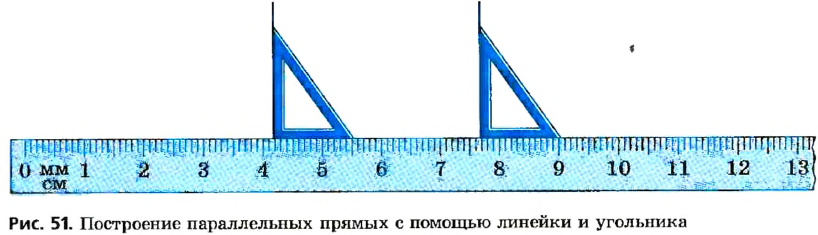
Свойство, описанное в теореме, используется для построения параллельных прямых с помощью линейки и угольника (рис. 51). Дважды прикладывая угольник к линейке, можно провести две прямые, перпендикулярные краю линейки. По доказанной теореме такие прямые параллельны.
Историческая справка
Древнейшая наука геометрия как и математика в целом, зарождалась из потребностей практической деятельности. Везде, где жили и работали люди, необходимо было измерять, вычислять, размышлять.
Первые документальные свидетельства о геометрических знаниях дошли до нас из Древнего Египта. Каждый год воды Нила затапливали почти все прибрежные земли, поэтому египтянам приходилось вновь их размежевывать. Именно так в процессе работы устанавливались простейшие свойства геометрических фигур.
Становление геометрии. Становление геометрии как строгой науки связано с работами древнегреческих ученых: Фалеса (ориент. 625-547 гг. до н.э.), Пифагора (ориент. 570-500 гг. до н. э.), Евдокса (ориент. 408-355 гг. до н. э.). Одной из выдающихся фигур в истории геометрии по праву считается Евклид Александрийский (ориент. 330-275 гг. до н. э.). Его произведение «Начала» стало учебником, по которому изучали геометрию на протяжении почти двух тысяч лет. Евклид первым применил именно тот подход к изложению геометрии, которым мы пользуемся сейчас: сначала сформулировал основные определения и свойства простейших фигур (аксиомы), а затем, опираясь на них, доказал многие другие утверждения.
Возведенные за две-четыре тысячи лет до нашей эры, египетские пирамиды и сегодня поражают точностью метрических отношений; строители уже тогда знали немало геометрических положений и расчетов.
Профессор Харьковского университета Алексей Васильевич Погорелое (1919-2002) обогатил современную геометрию новейшими исследованиями и создал школьный учебник, по которому занимались несколько поколений учащихся.
Исследования и открытия ученых- геометров нашли применение во многих областях человеческой деятельности. Геометрия стала элементом общечеловеческой культуры — ведь без знания основ геометрии невозможно представить себе современного просвещенного человека.
Герметрия в Украине Интересные страницы истории развития геометрии, в частности ее преподавания в школе, связаны с Украиной. Именно здесь, в одной из харьковских гимназий, в конце XIX в. начинал свою деятельность известный русский педагог Андрей Петрович Киселев (1852-1940). по учебнику которого изучали геометрию нэ протяжении почти 60 лет.
Справочный материал по простейшим геометрическим фигурам
1. Точки и прямые
- ✓ Основное свойство прямой. Через любые две точки можно провести прямую, и притом только одну.
- ✓ Две прямые, имеющие общую точку, называют пересекающимися.
- ✓ Любые две пересекающиеся прямые имеют только одну общую точку.
2. Отрезок и его длина
- ✓ Точки А и В прямой а (рис. 239) ограничивают часть прямой, которую вместе с точками А и В называют отрезком, а точки А и В — концами этого отрезка.
- ✓ Два отрезка называют равными, если их можно совместить наложением.
- ✓ Равные отрезки имеют равные длины, и наоборот, если длины отрезков равны, то равны и сами отрезки.
- ✓ Основное свойство длины отрезка. Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и СВ, то есть АВ = АС + СВ.
- ✓ Расстоянием между точками А и В называют длину отрезка АВ. Если точки А и В совпадают, то считают, что расстояние между ними равно нулю.
3. Луч. Угол
- ✓ Точка О прямой АВ (рис. 240) разбивает прямую на две части, каждую из которых вместе с точкой О называют лучом или полупрямой. Точку О называют началом луча.
- ✓ Два луча, имеющих общее начало и лежащих на одной прямой, называют дополнительными.
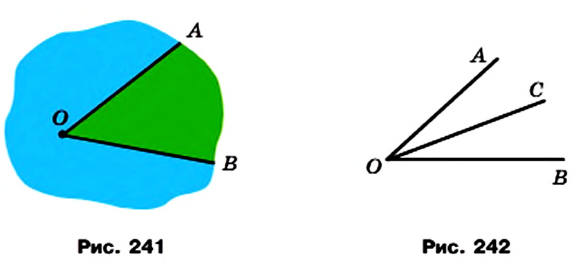
- ✓ Два луча ОА и ОВ, имеющие общее начало (рис. 241), разбивают плоскость на две части, каждую из которых вместе с лучами ОА и ОВ называют углом. Лучи ОА и ОВ называют сторонами угла, а точку О — вершиной угла.
- ✓ Угол, сторонами которого являются дополнительные лучи, называют развернутым.
- ✓ Два угла называют равными, если их можно совместить наложением.
- ✓ Биссектрисой угла называют луч с началом в вершине угла, делящий этот угол на два равных угла.
4. Измерение углов
- ✓ Каждый угол имеет определенную величину (градусную меру).
- ✓ Угол, градусная мера которого равна 90°, называют прямым. Угол, градусная мера которого меньше 90°, называют острым. Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
- ✓ Равные углы имеют равные величины, и наоборот, если величины углов равны, то равны и сами углы.
- ✓ Основное свойство величины угла. Если луч ОС делит угол АОВ на два угла АОС и СОВ (рис. 242), то
5. Смежные и вертикальные углы
- ✓ Два угла называют смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
- ✓ Сумма смежных углов равна 180°.
- ✓ Два угла называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого.
- ✓ Вертикальные углы равны.
6. Перпендикулярные прямые. Серединный перпендикуляр
- ✓ Две прямые называют перпендикулярными, если при их пересечении образовался прямой угол.
- ✓ Неперпендикулярные прямые при пересечении образуют пару равных острых углов и пару равных тупых углов. Величину острого угла называют углом между неперпендикулярными прямыми.
- ✓ Если прямые перпендикулярны, то считают, что угол между ними равен 90°.
- ✓ Два отрезка называют перпендикулярными, если они лежат на перпендикулярных прямых.
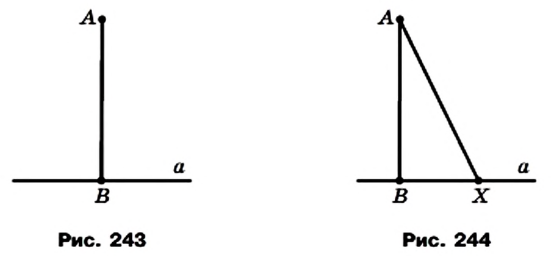
- ✓ На рисунке 243 изображены прямая а и перпендикулярный ей отрезок АВ, конец В которого принадлежит прямой а. В таком случае говорят, что из точки А на прямую а опущен перпендикуляр АВ. Точку В называют основанием перпендикуляра АВ.
- ✓ Длину перпендикуляра AB называют расстоянием от точки А до прямой а. Если точка А принадлежит прямой а, то считают, что расстояние от точки А до прямой а равно нулю.
- ✓Опустим из точки А на прямую а перпендикуляр АВ (рис. 244). Пусть X — произвольная точка прямой а, отличная от точки В. Отрезок АХ называют наклонной, проведенной из точки А к прямой а.
- ✓ Через данную точку проходит только одна прямая, перпендикулярная данной.
- ✓ Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.
- ✓ Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.
- ✓ Если точка равноудалена от концов отрезка, то она принадлежит серединному перпендикуляру этого отрезка.
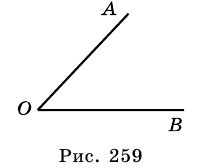
Элементарные геометрические фигуры и их свойства
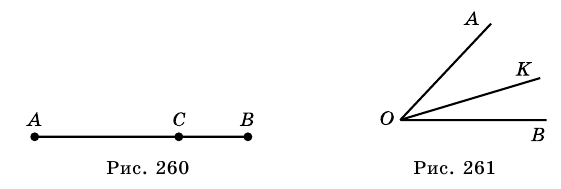
Основными геометрическими фигурами на плоскости являются точка и прямая.
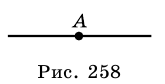
Отрезком называют часть прямой, которая состоит из всех точек этой прямой, которые лежат между двумя ее точками, вместе с этими точками. На рисунке 257: отрезок 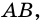
Точка 
вместе с точкой 
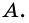
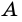
• Два луча, имеющие общее начало и дополняющие друг друга до прямой, называют дополняющими.
Угол — это геометрическая фигура, состоящая из двух лучей, которые выходят из одной точки. Лучи называют сторонами угла, а их общее начало — вершиной угла. На рисунке 259: угол 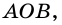
Биссектрисой угла называют луч, который выходит из вершины угла, проходит между его сторонами и делит его пополам.
Аксиомы планиметрии
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры — виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Треугольник
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
Геометрические фигуры. Полные уроки
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Геометрические фигуры. Полные уроки
Содержание
- 1 Тема урока
- 2 Что такое геометрическая фигура
- 3 Что такое геометрия
- 4 Точка
- 5 Прямая
- 6 Плоскость
- 7 Угол
- 8 Параллелограмм
- 9 Трапеция
- 10 Окружность и круг
- 11 Треугольник
- 12 Многоугольник
- 13 Интересные факты
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике.
Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
• Какая ломаная линия называется незамкнутой?
• Как обозначается прямая?
• Как называется ломаная линия, у которой четыре замкнутых звена?
• Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
Интересные факты
• А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
• Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
• «Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
• «Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
• А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
• А вот одна из известных картин, созданная еще в начале прошлого века Малевичем, прославляет такую геометрическую фигуру, как квадрат. Черный квадрат на белом фоне является мистической загадкой для окружающих, притягивая к себе исследователей и восхищенные взгляды живописцев.
Предмети > Математика > Математика 7 класс
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: