Gain all of the knowledge and skills that you need to get started in the optical and mechanical world.

Getting Started with OpticStudio
Explore the OpticStudio interface and the range of capabilities with these introductory resources. This is the jumping off point …
3 Hours

Getting Started with OpticsBuilder
Learn how to easily convert optical designs into CAD, analyze the affect mechanical components have on optical performance by per…
3 Hours

Getting Started with OpticsViewer
Discover how to view optical performance, prescription and manufacturing data in OpticsViewer. Follow these tutorials to master c…
2 Hours

Getting Started with ZOS-API
Getting Started with ZOS-API is designed to get you up to speed quickly with the powerful features of ZOS-API. This Learning Path…
5 Hours

ZPL Programming
The Zemax Programming Language (ZPL) allows users to write their own programs within OpticStudio.
These programs can:
Automate …
3 Hours

Designing with Holograms
This learning path covers everything you should know to effectively model holograms in OpticStudio. You will learn about the diff…
6 Hours

How to Build a Spectrometer
In this learning path, you will learn how to build a spectrometer. Spectroscopy is a non-invasive technique and one of the most p…
3 Hours

Modeling Laser Beam Propagation in OpticStudio
Learn the key steps in modeling laser beam propagation in OpticStudio. Discover what tools are available, how to set up, analyze …
5 hours

Imaging System Fundamentals
Learn the key steps in imaging system design with OpticStudio. Discover how to setup, analyze, optimise and tolerance a simple im…
3 Hours

Illumination Systems Fundamentals
This Learning Path will provide the fundamental skills necessary for illumination design to build on for more advanced tasks. Fir…
7 Hours
Gain all of the knowledge and skills that you need to get started in the optical and mechanical world.

Getting Started with OpticStudio
Explore the OpticStudio interface and the range of capabilities with these introductory resources. This is the jumping off point …
3 Hours

Getting Started with OpticsBuilder
Learn how to easily convert optical designs into CAD, analyze the affect mechanical components have on optical performance by per…
3 Hours

Getting Started with OpticsViewer
Discover how to view optical performance, prescription and manufacturing data in OpticsViewer. Follow these tutorials to master c…
2 Hours

Getting Started with ZOS-API
Getting Started with ZOS-API is designed to get you up to speed quickly with the powerful features of ZOS-API. This Learning Path…
5 Hours

ZPL Programming
The Zemax Programming Language (ZPL) allows users to write their own programs within OpticStudio.
These programs can:
Automate …
3 Hours

Designing with Holograms
This learning path covers everything you should know to effectively model holograms in OpticStudio. You will learn about the diff…
6 Hours

How to Build a Spectrometer
In this learning path, you will learn how to build a spectrometer. Spectroscopy is a non-invasive technique and one of the most p…
3 Hours

Modeling Laser Beam Propagation in OpticStudio
Learn the key steps in modeling laser beam propagation in OpticStudio. Discover what tools are available, how to set up, analyze …
5 hours

Imaging System Fundamentals
Learn the key steps in imaging system design with OpticStudio. Discover how to setup, analyze, optimise and tolerance a simple im…
3 Hours

Illumination Systems Fundamentals
This Learning Path will provide the fundamental skills necessary for illumination design to build on for more advanced tasks. Fir…
7 Hours
Время на прочтение
9 мин
Количество просмотров 56K
Построение идеальной оптики в Zemax
Введение
Всё больше современные системы автоматизации оснащаются оптическими устройствами для решения задач позиционирования, распознавания, наблюдения и др. Построение идеальных оптических систем при помощи программы расчета Zemax может оказаться полезным и непрофессионалам, например, для лучшего понимания теории, особенностей оптических устройств и выполнения прикидочных расчетов оптических систем. В этой работе рассмотрены приёмы построения идеальной оптики в среде Zemax, даны примеры расчета диапазона автофокусирования фотокамеры, построения эквивалентной схемы монокуляра МГТ 2.5×17.5, объектива фотокамеры SUNNY P13N05B смартфона Huawei P7 и замены идеальных оптических элементов реальными.
Идеальная оптика
Изображение в идеальной оптике, в которой отсутствуют искажения, строится по законам параксиальной оптики. Термин параксиальный означает «вблизи оси». Параксиальная оптика хорошо описываются линейными выражениями, которые при малых углах заменяются линейными уравнениями. В параксиальной области любая реальная система ведет себя как идеальная.
Расчеты идеальных линз в среде Zemax выполняются с допущением, что линзы имеют параксиальные свойства не только вблизи оси, но и на всей рабочей поверхности, которая действует как идеальная тонкая линза c единичным показателем преломления воздуха.
Параксиальную оптику целесообразно использовать в качестве эталона, с которым сравниваются аберрации (искажения) реальной оптики.
Переносить результаты расчетов параксиальной оптики на реальные системы следует с осторожностью, особенно при построении систем у которых свойства вблизи оптической оси и на удалении значительно отличаются.
Разработан целый ряд приёмов уменьшения аберраций и габаритных размеров линз: применение несферических поверхностей, составных линз, неоднородных оптических материалов, и др. Но как не была бы устроена реальная линза (Петцваля, Гаусса, Барлоу, …) ее характеристики могут только приближаться к характеристикам идеальной линзы.
Построение изображения собирающей линзой
Рассмотрим случай, когда от каждой точки плоскости предмета расходятся лучи во все стороны как от точечных источников. Из крайней точки объекта А, как показано на Рис. 1. в соответствующую точку В на плоскости изображения попадут только те лучи, которые сфокусированы линзой. Количество лучей предмета попадающих в плоскость изображения пропорционально диаметру линзы. Чем больше лучей от предмета попадает в плоскость изображения, тем выше яркость изображения.
Рис. 1. Сопряженные точки. Ход лучей от точки предмета к соответствующей точке
изображения на плоскости фотоприемника.
Для минимизации вычислений нахождения изображения рассматривают ход только нескольких лучей, например, как на Рис. 2: луч, идущий от объекта вдоль оптической оси; луч, проходящий через центр линзы и луч, параллельный оптической оси, преломляемый линзой и проходящий через главный фокус линзы (точка F на оптической оси).
Рис. 2. Минимальные построения для нахождения расстояния до плоскости изображения, величины изображения и увеличения линзы. Для параксиальной оптики продольное увеличение (связано с расстояниями) равно квадрату линейного увеличения (перпендикулярно оси), а угловое увеличение обратно пропорционально линейному.
Связь расстояний до предмета и изображения. Глубина резкости
Построение зависимости между зоной фокусировки объектива и глубиной резкости в пространстве предметов [1] показано на Рис. 3. Когда расстояние до предмета равно бесконечности, плоскость сфокусированного изображения проходит через главный фокус (смещение плоскости изображения относительно фокуса равно нулю). Минимальная глубина резкости в пространстве предметов достигается при максимальном удалении плоскости изображения (в зоне фокусировки) относительно главного фокуса.
Рис. 3. Зависимость между зоной фокусировки объектива и глубиной резкости в пространстве предметов.
Функции среды проектирования Zemax
Функции среды Zemax, наиболее часто используемые при проектировании оптических систем, присвоены отдельным кнопкам основного меню. Назначение этих кнопок показано на Рис. 4.
Рис. 4. Интерфейс программы Zemax.
Типы поверхностей элементов оптических систем, радиусы поверхностей, расстояния между элементами и другие параметры заносятся в таблицу редактора, в которой каждая строка содержит параметры одного элемента. Связь параметров таблицы и элементов оптической схемы показана на примере Рис. 5.
Рис. 5. Связь оптической схемы с параметрами таблицы.
Идеальная линза в Zemax
Для моделирования линзы с параксиальной поверхностью в Zemax необходимо задать фокусное расстояние и, при необходимости, включить расчет разницы оптических траекторий проходящих через линзу (установить статус OPD режима в 1 в соответствующей строке таблицы редактора). По умолчанию, OPD расчет не выполняется (статус OPD равен нулю [2]).
Построим в Zemax идеальную линзу, например, с диаметром входного зрачка 10 мм и фокусным расстоянием 15 мм, собирающую параллельные лучи удаленного предмета в одной точке.
1. Откроем новую таблицу: меню > кнопка
Рис. 6. Начальное состояние таблицы оптической схемы редактора Zemax. В строках таблицы (NN 0; 1 и 2) содержатся параметры предмета OBJ, апертурной диафрагмы STO и изображения IMA.
2. Добавим поверхность между диафрагмой и изображением: выделим последнюю строку строку IMA > меню Lens Data Editor > Edit > Insert Surface
Рис. 7. Добавлена стандартная поверхность N2.
3. Выберем «Параксиальный» тип поверхности: строка N2 > колонка Surf:Type > окно свойства — Properties > Surface Type > Paraxial
Рис. 8. Поверхность N2 изменена на идеальную (Paraxial) линзу с фокусным расстоянием 100 мм. Расстояние между линзой и изображением равно нулю. Расстояние между линзой и диафрагмой STO также равно нулю.
4. Изменим фокусное расстояние со 100 (по умолчанию) на 15 мм в колонке таблицы Focal Length
5. Зададим расстояние 15 мм от линзы до изображения в колонке Thickness
Рис. 9. Фокусное расстояние линзы изменено на 15 мм. Расстояние между линзой и изображением увеличено до 15 мм.
6. Зададим диаметр входного зрачка 10 мм: Основное меню > кнопка > закладка Aperture > Aperture Value > 10
Рис. 10. Задан диаметр входной апертуры оптической схемы: 10 мм.
7. Построим оптическую схему: Основное меню > кнопка
Рис. 11. Оптическая схема в окне Layout. Координаты диафрагмы и линзы совпадают (расстояние между ними равно нулю) Координаты “мышки” на схеме (в масштабе оптической схемы) отображаются в заголовке рисунка.
8. На схеме Layout не показаны лучи слева от идеальной линзы (выделена красным), идущие от предмета расположенного на бесконечном расстоянии, которое обозначено как Infinity в колонке Thickness нулевой строки OBJ таблицы. Чтобы показать часть этих лучей на входе линзы введем поверхность на расстоянии, например, 7 мм перед апертурной диафрагмой STO.
Рис. 12. Добавлена поверхность перед апертурной диафрагмой STO.
9. Добавим поверхность 1 к отображаемой части оптической схемы и увеличим количество лучей до 7 для наглядности: меню рисунка Layout > Setting > First Surface = 1 > Number of Rays = 7.
Рис. 13. Показаны лучи на отрезке 7мм до диафрагмы. Увеличено количество лучей с 3-х до 7.
10. Сделаем невидимой первую поверхность: строка N1 таблицы > колонка Surf:Type > окно свойства — Properties > закладка Draw >
11. Обновим окно Layout оптической схемы через кнопку основного меню или дважды «кликнув» в зоне окна схемы.
Рис. 14. Первая поверхность оптической схемы сделана невидимой.
В окне Layout можно отслеживать изменения табличных параметров оптической системы и параметров основного меню, показанных на Рис. 4 и Рис. 5.
Модель составной линзы фотокамеры смартфона
Для построения идеальной модели возьмем составную линзу фотокамеры SUNNY P13N05B смартфона Huawei P7 (Рис. 15). Линза смартфона состоит из пяти пластиковых элементов. Пример составной линзы показан на Рис. 16.
Рис. 15. Размеры [3] и фотографии фотокамеры SUNNY P13N05B с фотодиодной матрицей SONY IMX214 13 МП. 1. – модуль фотокамеры с фотодиодной матрицей; 2- линза камеры; 3 – катушка привода автофокусировки — перемещения объектива относительно матрицы датчика.
Камера P13N05B имеет следующие характеристики.
• Размер линзы: 1/3”
• Размер фотодиодной матрицы: 6,1 мм (H) × 4,5 мм (V)
• Диагональ активной зоны матрицы: 5,9 мм
• Состав линзы: 5 пластиковых элементов (см. Рис. 16)
• Фокусное расстояние: 3,79 мм
• Апертурное число (f/#): 2
• Угол поля зрения: 75°±3°
• Глубина резкости: от 7 см до ∞
• Диапазон привода автофокусировки: ≥ 0,24mm
Рис. 16. Пример составной линзы. Линза смартфона iPhone 6.
Параметры оптической схемы идеального объектива фотокамеры (см. Рис. 17) заданы в таблице Lens Data Editor и в окнах клавиш основного меню Zemax:. Функция выбираемая из списка функций выделенной ячейки колонки Thickness таблицы автоматически устанавливает наилучшее расстояние между линзой и изображением. Для построения наилучшего изображения удаленного на бесконечное расстояние предмета плоскость фотоприёмника должна проходить через точку главного фокуса отстоящей от линзы на 3,79 мм.
Рис. 17. Оптическая схема параксиальной линзы фотообъектива. Предмет удален на бесконечное расстояние.
Приближение объекта к линзе на 10 мм с сохранением угла обзора 76о/2 в окне Field Data (Рис. 18) увеличило расстояние между линзой и изображением до 6,10 мм. Следовательно изменение автофокуса при приближении объекта с бесконечности до 10 мм равно 2,31 мм (как 6,10 мм – 3,79 мм).
Рис. 18. Построение лучей от объекта находящегося в 10 мм от параксиальной линзы фотокамеры и нахождение положения автофокуса.
В спецификации фотокамеры P13N05B указано, что глубина резкости в пространстве предметов лежит в пределах от 7 см до ∞ (бесконечности). Установим предмет на минимальной дистанции в 70 мм от апертурой линзы. Zemax устанавливает расстояние между линзой и плоскостью изображения 4 мм (см. выделенную ячейку таблицы на Рис. 19). Таким образом, для построения качественного изображения предмета находящегося в зоне от 7 см до ∞ требуется изменять расстояние между линзой и фотодатчиком от 4 до 3,79 мм. Требуемое изменение 0,21мм перекрывается диапазоном привода автофокусировки фотокамеры 0,24 мм.
Рис. 19. Расстояние до изображения равно 4 мм при расстоянии до объекта 70 мм. Фокусное расстояние линзы равно 3,79 мм.
Зависимость диапазона фокусировки от фокусного расстояния объектива
Зона фокусировки зависит не только от дистанции до предмета, но и от главного фокуса линзы (объектива). На Рис. 20 показана геометрия нахождения зон фокусировки для линз с главным фокусом F1=7,5 мм и F2=19 мм и положений предмета в диапазоне AB = 35… 52 мм. Для настройки резкости с линзой F1 требуется изменять расстояние меду главным фокусом линзы и плоскостью изображения в диапазоне 0,8 мм, тогда как для линзы с F2 этот диапазон вырос до 12 мм.
Рис. 20. Пример построения зон фокусировки для линз с разными фокусными расстояниями F1 и F2.
Идеальные телескопы
Сравнительные размеры телескопов Кеплера и Галилея для одинакового увеличения F1/F2 показаны на Рис. 21. Телескоп Кеплера с собирающими линзами даёт перевернутое изображение. Более компактный телескоп Галилея включает рассеивающую линзу и даёт прямое изображение.
Рис. 21. Схема телескопов Кеплера (а) и Галилея (б) при одинаковом увеличении F2/F1.
Миниатюрный монокуляр МГТ 2,5×17,5 СССР, ЛЗОС (Лыткаринский завод оптического стекла) собран по схеме Галилея (Рис. 22). Он имеет следующие характеристики.
• Увеличение: 2,5 крат(раз)
• Диаметр объектива: 17,5 мм
• Угол поля зрения: 13,5 град
• Разрешающая способность: 15 угл. сек
• Предел фокусировки окуляра: -5…+5 диоптр
• Габаритные размеры: 22 x 38 мм
Рис. 22. Вид и примерные размеры миниатюрного монокуляра МГТ 2,5×17,5. Предмет находится справа.
Эквивалентная идеальная оптическая схема монокуляра МГТ 2,5×17,5 в ZEMAX показана на Рис. 23. Схема состоит из собирающей и рассеивающей линз с главными фокусами 37,5 мм и -15 мм соответственно, имеющими отношение 2,5 раз. Диаметр собирающей линзы 2х8,75 мм.
Рис. 23. Табличные данные и идеальная оптическая схема монокуляра МГТ 2,5×17,5. Параллельные лучи идут от предмета удаленного на бесконечное расстояние.
Вариант замены параксиальной линзы реальной
Заменим первую параксиальную линзу (диаметр: 17,5 мм; фокусное расстояние: 37,5 мм) монокуляра ахроматической линзой из каталога Edmund Optics [4]. Чтобы минимизировать выборку линз установим следующие условия: категория — Achromatic Lenses; диаметр – 18 мм; эффективная фокальная длина EFL 30-39.99 мм; диапазон длин волн — 425 — 675 нм.
Ближайшая к требуемым параметрам линза: 18mm Dia. x 35mm FL, VIS 0° Coated, Achromatic Lens, Stock No. #47-706 (номер по каталогу).
Для построения ахроматической линзы в Zemax из ее спецификации возьмем параметры перечисленные в Таблица 1. Параметры можно найти и на чертеже линзы PDF drawing сайта Edmund Optics [4] или на Рис. 24.
Таблица 1. Параметры составной ахроматической линзы Edmund #47-706
| Параметр | Значение | Примечание |
|---|---|---|
| Diameter | 18,0 мм | Диаметр |
| Clear Aperture CA | 17,0 мм | Диафрагма |
| Effective Focal Length | 35,0 мм | Эффективное фокусное расстояние |
| Center Thickness CT 1 | 6,01 мм | Толщина 1-го элемента по оси |
| Center Thickness CT2 | 1,60 мм | Толщина 2-го элемента по оси |
| Radius R1 (mm) | 24,26 мм | Радиус первой поверхности |
| Radius R2 (mm) | 16,23 мм | Радиус второй поверхности |
| Radius R3 (mm) | -152,99 мм | Радиус третьей поверхности |
| Substrate | N-BAF10 / N-SF10 | Материалы элементов |
Рис. 24. Чертеж ахроматической линзы Edmund #47-706.
Замена параметров первой линзы идеального телескопа (строка N2 таблицы Рис. 23) линзой Edmund #47-706 даёт вариант, представленный на Рис. 25.
Рис. 25. Вариант оптики телескопа с реальной ахроматической линзой. Выделенное в таблице красным расстояние между линзами найдено ручным смещением движка Slider.
Расстояние между линзами (выделенное красным в таблице Рис. 25) изменялось ползунком Slider в ручную до момента когда лучи на выходе второй (идеальной линзы) установились параллельными главной оси (в этом положении фокусные расстояния линз телескопа находятся в одной точке). Действие ползунка в реальном времени отображается смещением элементов оптической схемы и изменением траекторий лучей на оптической диаграмме окна Layout. Ползунок можно открыть через основное меню Zemax > Tools > Miscellaneous > Slider.
Если на выходе телескопа поставить дополнительную параксиальную собирающую линзу (элемент N6 в таблице и красная плоскость на оптической схеме Рис. 26), то можно увидеть вносимые реальной линзой искажения (см. часть диаграмм Zemax на Рис. 26).
Рис. 26. Оптическая схема и диаграммы искажений, вносимые реальной линзой.
Литература
1. Сайт Optics Realm. Видеоуроки по проектированию в среде Zemax и теории оптики. www.opticsrealm.com
2. Zemax Help > Optical Design Program User’s Guide .pdf
3. H&L ELECTRICAL MANUFACTORY LIMITED hnl.en.e-cantonfair.com/products/sunny-brand-p13n05b-imx214-sony-sensor-13-0m-pixel-mipi-csi-1080p-sunny-cmos-camera-module-552104.html
4. Edmund Optics. www.edmundoptics.com/optics/optical-lenses
5. Dr. Bob Davidov. Компьютерные технологии управления в технических системах portalnp.ru/author/bobdavidov.

U». Буква «U» означает, что величина этого параметра установлена пользователем (User). Если буква «U» отсутствует, то это означает, что ZEMAX вычисляет величину этого параметра в соответствии с требуемой величиной апертуры. Вы можете убрать букву «U», нажав клавиши Ctrl-Z или дважды кликнув мышкой на колонку Semi-Diameter и выбрав опцию «Automatic». После сделанных изменений выберите из главного меню System, Update для обновления данных. Установленная нами величина 14 относится к полудиаметру, а диаметр линзы будет равен 28 мм. Таким же образом введите числа 14 для поверхностей 2 и 3.
Обновить окно с изображением оптической схемы. Теперь апертуры увеличились, но краевая толщина первой линзы стала отрицательной величиной! Обновить окно с данными о поверхности, чтобы увидеть новое значение ее краевой толщины; оно стало отрицательным числом. Чтобы сделать краевую толщину линзы разумной величиной, можно было бы увеличить ее центральную толщину. Однако имеется более мощный метод задания требуемой величины для краевой толщины линзы.
Предположим, что хотим сделать краевую толщину линзы равной 3 мм. Чтобы сделать это, дважды кликните мышкой на колонку толщины в строке 1 поверхности. На экране появится диалоговое окно для установки статуса поверхности. Выберите опцию «Edge Thickness» (краевая толщина) и «Radial Height»
(радиальная высота). Установите толщину 3 и радиальную высоту 0 (если радиальная высота равна нулю, то ZEMAX использует заданную величину полудиаметра); нажмите на ОК. В таблице редактора LDE автоматически установится новая величина толщины поверхности 1. Появившаяся рядом с этой величиной буква «Е» означает, что на этот параметр наложено специальное условие.
Обновите снова окно с данными о поверхности, и увидите, что в нем указана краевая толщина поверхности, равная 3.
Можно также обновить все окна сразу, выбрав из главного меню System, Update All. Это приведет к обновлению схемы и графиков аберраций. Установив новую величину толщины, тем самым несколько изменили фокусное расстояние системы. Посмотрите сейчас на график аберраций. Затем запустите алгоритм оптимизации (выберите Tools, Optimization и режим «Automatic»). После оптимизации выйдите из режима оптимизации, нажав на «Exit», выберите в главном меню System и Update All для обновления графиков.
Хотим проверить внеосевые характеристики дублета. Из главного меню выберите System. Fields (поля) для входа в диалоговое окно «Field Data»(дaнныe поля зрения). Откройте три поля, нажав в колонке «Use» (использовать) на 2 и 3 ряды втором ряду колонки Y-поля введите число 7 (семь градусов) и в третье введите число 10. Оставьте в первом ряду нулевое значение для осевого направления. Оставьте также нулевые значения в рядах X поля; для систем с вращательной симметрией эти направления имеют небольшое значение. Нажмите на ОК для закрытия диалогового окна.
Теперь выберите System, Update All. Появится график аберраций, показанный на рис. Е2- 4. График может слегка отличаться от показанного на этом рисунке в зависимости от того, как прошла реоптимизация системы после введенных функций solves.
Заключение. Внеосевые характеристики являются очень плохими. Дело в том, что мы оптимизировали схему для осевого направления. Какие аберрации теперь ограничивают ?
Анализ графика аберраций показывает, что главная аберрация — это кривизна поля. Величину этой аберрации можно оценить по графику кривизны поля. Выберите из главного меню Analysis, Miscellaneous, Field Curv/Dist (Кривизна поля / Дисторсия). Появится график,
показанный на рис. Е2-5.

Левый график изображает величины смещения параксиального фокуса в зависимости от угла поля, а правый дисторсию реальных лучей относительно параксиального луча. Вся информация для графика кривизны поля получена из данных об аберрациях. График кривизны поля пропорционален наклонам в начале координат графика аберраций. Существуют методы коррекции кривизны поля, а также сферической аберрации и комы. Эти методы описаны в книге Smith, Modern Optical
Engineering.
2.Требования к содержанию отчета. Отчет должен содержать:
— цель работы, — провести генерирование оптических схем,
— построить графики кривизны поля, — выводы.
3.Контрольные вопросы
1.Как провести генерирование оптических схем.
2.Какие графики кривизны поля.
3.Как задать ограничения на краевую толщину линзы, задание углов поля.
К ЛАБОРАТОРНОЙ РАБОТЕ № 3
Изучаются: использование зеркал, конических постоянных, поверхностей типа «Coordinate breaks», изображение схемы в трехмерной проекции. Экранирование.
Если проработали два предыдущих примера, то должны быть готовы к созданию более сложных схем. Телескоп Ньютона — простейшая схема телескопа с исправленными осевыми аберрациями; она служит хорошей иллюстрацией для понимания некоторых фундаментальных операций при работе с ZEMAX. Прежде всего, телескоп Ньютона — это система, содержащая простое параболическое зеркало и ничего больше. Парабола полностью устраняет сферические аберрации всех порядков, и так как будем использовать телескоп только для работы на оси, то других аберраций нет. Для начала закройте все окна, за исключением окна LDR, и выберите из главного меню File, New (новый).
Положим, мы хотим спроектировать F/5 телескоп с фокусным расстоянием 1000 мм. Это предполагает использование зеркала с радиусом кривизны 2000 мм и апертурой 200 мм. Установим курсор в колонку радиуса кривизны в строку поверхности 1, которая обозначена как STOP, и введем число -2000,0; знак минус означает, что зеркало будет обращено своей вогнутой поверхностью в сторону объекта. Теперь для этой же поверхности введем толщину — 1000; знак минус означает, что после отражения от зеркала лучи будут идти в противоположном направлении. Напишем для этой же поверхности в колонке «Glass» слово «MIRROR» (зеркало). Теперь из главного меню выберем System, General (главные параметры) и в открывшемся диалоговом окне напечатаем число 200 для величины апертуры системы. Нажмите на ОК.

По умолчанию ZEMAX будет использовать только одну длину волны — 0,55 мкм и только одно направление в поле зрения — 0 градусов, но для наших целей этого достаточно. Откроем теперь окно с изображением оптической схемы. Лучи идут от первой поверхности к плоскости изображения, которая теперь находится слева от зеркала. Если теперь вызвать диаграмму пятна рассеяния (Analysis, Spot Diagrams. Standard; или клавиши Ctrl-S). то увидите большое пятно рассеяния со среднеквадратической величиной радиуса рассеяния 77.6 мкм. Удобный способ для оценки качества изображения — это построение на диаграмме пятна рассеяния дифракционного кружка Эйри. Для этого выберите опцию Settings (установки) в меню окна Диаграммы Рассеяния и в опции «Show Scale» (показать шкалу) установите Airy Disk (диск Эири), нажмите на ОК В результате Вы увидите диаграмму, показанную на рисунке Е3-1.
На диаграмме указано, что среднеквадратическая величина радиуса рассеяния равна 77,6 мкм. То, что наша система сейчас еще не имеет дифракционного качества, обусловлено тем, что еще не ввели величину конической постоянной (-1) для задания параболы. В колонке «Conic» введем для поверхности 1 число -1 и нажмем на клавишу Enter. Теперь обновим все окна, используя System, Update All. На обновленной диаграмме пятна рассеяния должны увидеть большой круг Эйри с крошечным скоплением лучей в центре. Среднеквадратический радиус пятна рассеяния равен нулю.
К сожалению, это высокое качество изображения получается в неудобном месте: из—за существования входящего в систему пучка лучей изображение получается недоступным для наблюдения. Этот недостаток обычно исправляется путем введения в систему поворотного плоского зеркала, установленного после главного зеркала. Наклоненное на 45 градусов поворотное зеркало вынесет плоскость изображения в сторону от оптической оси. Для введения в систему поворотного зеркала должны сначала решить, где оно должно быть расположено. Так как ширина входящего пучка лучей равна 200 мм, должны удалить плоскость изображения от оси по меньшей мере на 100 мм. Выберем это расстояние равным 200 мм, и тогда поворотное зеркало должно находиться на расстоянии 800 мм от главного зеркала.
Начнем с изменения величины толщины поверхности 1, которую установим равной -800. Теперь переместим курсор на поверхность изображения и нажмем клавишу Insert для введения новой поверхности, на которой будет расположено поворотное зеркало. Введем для толщины этой поверхности число -200, чтобы общее расстояние от главного зеркала до плоскости изображения было равно -1000.
Теперь кликните мышкой на Tools. Add Fold Mirror (добавить поворотное зеркало), установите в табличке «fold surface» цифру 2 (поверхность 2) и нажмите на ОК. Результирующая таблица LDE будет выглядеть как показано ниже (некоторые колонки для краткости не показаны).
Теперь посмотрим, как выглядит новая система Ньютона с поворотным зеркалом. Использовавшееся нами раннее окно с изображением схемы больше не будет работать (оно работает только с системами, обладающими осевой симметрией), и должны теперь вместо него использовать новое окно, дающее трехмерное изображение схемы, открыв его через Analysis, Layout. 3D Layout. При появлении трехмерного изображения схемы используйте клавиши компьютера <, ^, >, Page Up и Page Down для поворота схемы относительно трех осей. ZEMAX позволяет поворачивать изображение в соответствии с поворотом схемы Одна из возможных проекций трехмерной схемы показана на рис. ЕЗ-2.

Вид этой проекции может быть улучшен несколькими путями. Прежде всего, могут быть показаны лучи, идущие от объекта к зеркалу. Могут быть также экранированы лучи, падающие на тыльную сторону поворотного зеркала, с тем, чтобы они не достигали плоскости изобра— жения. Это важный эффект для реальных систем, так как лучи физически не могут пройти через поворотное зеркало в обычных оптических системах.
Во—первых, добавим одну пустую поверхность перед поверхностью апертурной диафрагмы, нажав на клавишу «Insert» при положении курсора в строке поверхности 1. Теперь сделаем толщину этой пустой поверхности равной 900. Затем дважды кликнем мышкой на слово «Standard» на поверхности 1. В открывшемся диалоговом окне выберем опцию «Circular Obscuration» (круглый экран) из меню «Aperture Type» (тип апертуры). Это позволяет поместить в пучок круглый экран, который будет экранировать часть пучка, падающего на тыльную сторону поворотного зеркала. Для величины максимального радиуса («Max Radius») введем число 40 и затем нажмем на ОК.
Теперь обновим 3D схему. Теперь система выглядит более реалистичной, — как показано на рис. ЕЗ-3. Если на схеме видны не все поверхности, выберите из меню этого окна опцию Setting и измените в открывшемся окне номера первой (first) и последней (last) поверхностей на 1 и 6 соответственно (или просто нажмите на элемент со словом Reset), а затем нажмите на ОК.
Описанная здесь процедура — это все, что требуется для введения в систему поворотных зеркал. Использованные нами
фиктивные поверхности «Coordinate breaks» могут быть использованы также для наклона и децентрировки любых других оптических элементов Целые группы оптических элементов могут быть наклонены или децентрированы таким способом; смотри примеры схем, включенных в библиотеку образцов ZEMAX.
2. Требования к содержанию отчета.
Отчет должен содержать:
—цель работы,
—расчеты и схемы ,
—выводы.
3. Контрольные вопросы
1 Как используются зеркала, конические постоянные, поверхностей типа «Coordinate
breaks».
2. Изобразите схемы в трехмерной проекции. Экранирование.
К ЛАБОРАТОРНОЙ РАБОТЕ № 4
Изучаются: Использование полиномиальных асферических поверхностей, экранирование, апертуры статус параметров, оптимизацию, изображение схем, графики модуляционной передаточной функции.
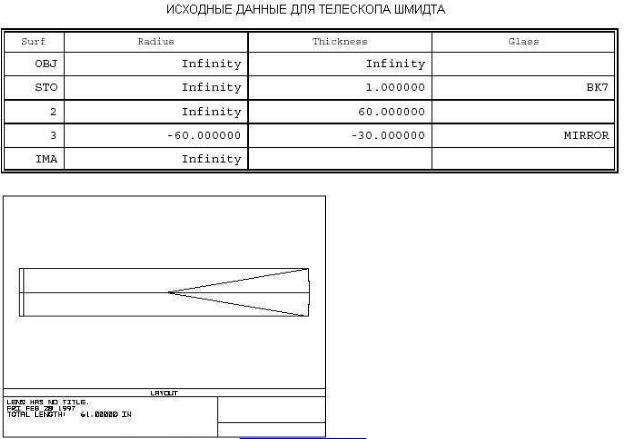
Эта глава посвящена полной схеме телескопа Шмидта с полиномиальным асферическим корректором. Предполагается, что схема будет использована для работы в видимой области спектра. Хотели бы иметь такой телескоп с апертурой 10 дюймов (inches) и величиной (заднего) фокусного расстояния 10 дюймов (от вершины главного зеркала до фокуса).
Проще всего в этой схеме начать с определения параметров корректора и главного зеркала, так что начнем с добавления в таблицу LDE двух поверхностей после поверхности STOP. Из главного меню выберем System, General и введем число 10 для величины апертуры. В этом же окне изменим единицы измерения с миллиметров («Millimeters») на дюймы («Inches»).
Из главного меню выберем System, Wavelength для входа в диалоговое окно Wavelength Data и установим в нем три длины волны 0,486; 0.587 и 0,656 с главной длиной волны 0.587. Введение этих трех длин волн может быть сделано одним шагом: нажмите в нижней части этого окна на элемент «Select -:
Сейчас будем использовать установленное по умолчанию направление в поле зрения 0 градусов. Введите теперь данные в таблицу LDE так, как это показано в нижеследующей таблице.
Апертурная диафрагма системы расположена в центре кривизны главного зеркала; это сделано для устранения полевых аберраций (типа комы) и характеризует схему Шмидта. Теперь выведем на экран изображение схемы для проверки, что все сделано правильно. Стандартная 2D схема будет прекрасно работать. Должны увидеть такую же схему, как изображено на рис. Е4-1.
Теперь добавим в систему вторичное
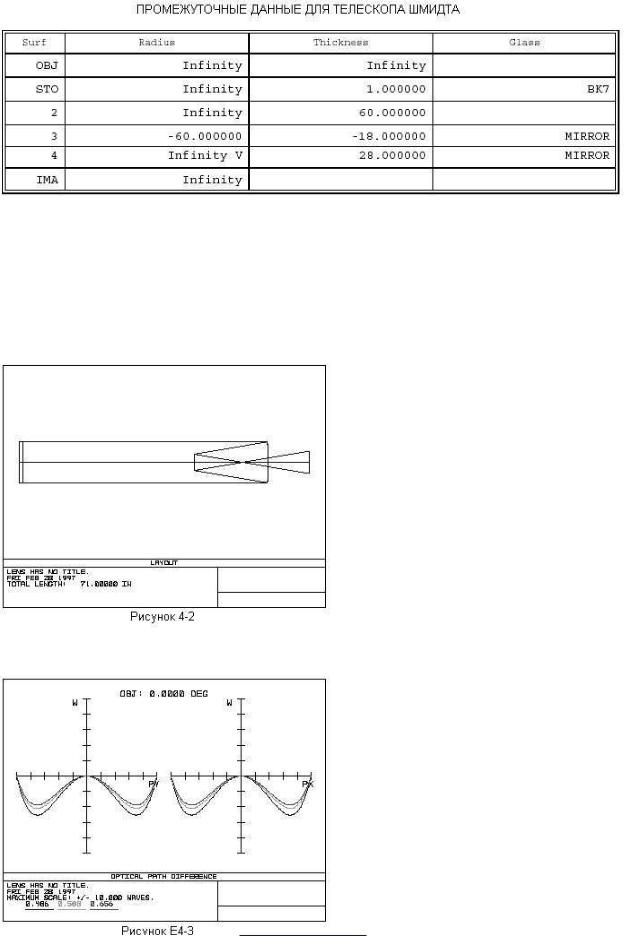
зеркало и определим положение плоскости изображения. Позже мы предоставим программе ZEMAX самой вычислить правильную величину кривизны вторичного зеркала. А сейчас модифицируем таблицу LDE, введя в нее одну новую поверхность, как показано в следующей ниже таблице.
Обратите внимание на то, что уменьшили расстояние от главного зеркала до -18. Это позволит держать под контролем размер вторичного зеркала. Расстояние до плоскости изображения теперь равно 20, так что величина расстояния от главного зеркала до плоскости изображения точно равна 10. Дополнительно был установлен статус переменной величины на радиус поверхности 4; мы дадим программе возможность самой найти правильную величину кривизны этой поверхности. Так как величина кривизны на эту поверхность не была установлена, то изображение сейчас не сфокусируется на плоскость изображения. Проверьте правильность выполненной работы путем рассмотрения обновленной схемы. Она должна выглядеть как на рис. Е4-2.
Теперь из главного меню выберите
Editors. Merit Function (оценочная функция)
для выведения на экран редактора оценочной функции Из меню окна редактора выберите
Tools. Default Merit Function. Нажмите на клавишу с надписью «Reset», а затем установите в опции «Rings» число 5. Нажмите на ОК. Опция Rings определяет плотность лучей, которая будет использована в дальнейших расчетах, а наша схема требует большей плотности, чем устанавливается (по умолчанию) числом 3.
Из главного меню выберите Tools, Optimization. В открывшемся окне оптимизации выберите опцию «Automatic» и оценочная функция быстро уменьшится до примерно 1,3. Это оставшиеся ошибки волнового фронта.
Нажмите на «Exit» а затем System и Update AIl
Величина радиуса вторичного зеркала изменилась от бесконечно большой величины до -41,83.
Теперь выведем на экран график волновых аберраций (OPD), выбрав из главного меню Analysis, Fans, Optical Path Difference. График OPD показывает наличие в системе дефокусировки и сферической аберрации, — как это показано на рис. Е4-3.
Обратите внимание на то, что еще подлежит коррекции примерно 4%.
Теперь кликните мышкой на элемент таблицы с надписью «Standard» в строке поверхности 1. В появившемся диалоговом окне выберите «Even Asphere». Этот тип поверхности позволяет вводить величины коэффициентов полинома, описывающего асферическую поверхность, которая может быть использована для асферической коррекции; нажмите на ОК. Теперь переместите курсор в правую часть таблицы до появления колонки под названием «4th Order Term» в строке поверхности 1 и нажмите клавиши Ctrl-Z. Этим будет установлен статус переменной величины для этого параметра. Установите таким же образом статус переменности для коэффициентов 6-го («6th Order Term») и 8-гo (8th Order Term») порядков.
Теперь выберем из главного меню Tools, Optimization и нажмем на «Automatic». В течение нескольких секунд величина оценочной функции существенно уменьшится в результате произведенной ZEMAX компенсации сферической аберрации путем подбора коэффициентов асферичности различных порядков. Нажмите на Exit.
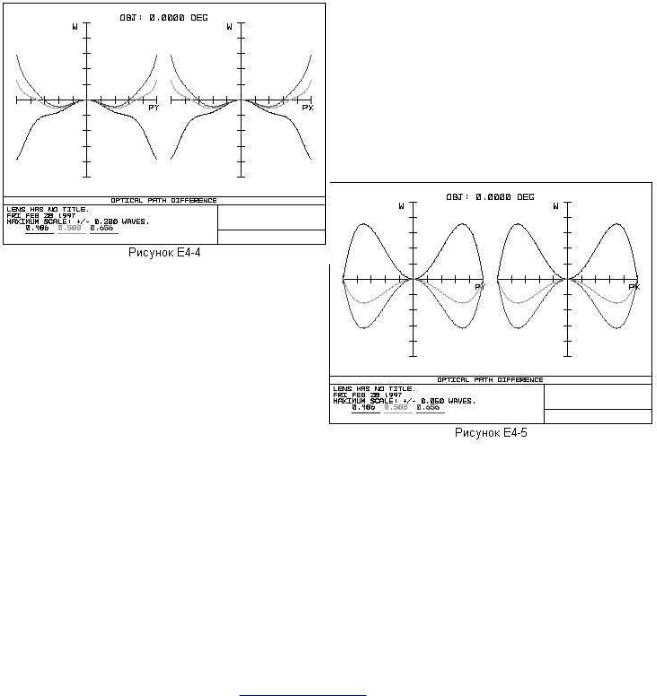
Теперь снова обновите график OPD: он показан на рис. Е4-4. Как видно, сферические аберрации существен но уменьшились. Обратите внимание на то, что теперь доминируют хроматические аберрации; на каждой длине волны сферические аберрации имеют различную величину. Это называется сферохроматизмом, и вскоре займемся его исправлением.
Нужен небольшой опыт для решения вопроса о том, как это лучше сделать. Для исправления сферохроматизма необходимо сбалансировать продольный хроматизм. Это общий подход при проектировании оптических систем; сюда же относится и задача компенсации аберраций высокого порядка аберрациями низкого порядка.
Для внесения продольного хроматизма будем варьировать величину кривизны поверхности 1 — передней поверхности пластины корректора (это позволит также упростить ее изготовление).
Установите сейчас статус переменной величины на радиус поверхности 1. Теперь
|
вновь проведем |
оптимизацию |
(Tools, |
|
Optimization, |
Automatic). |
Величина |
оценочной функции снова уменьшится.
Нажмите на Exit и обновите график OPD. Новый график должен выглядеть таким, как показано на рис. Е4-5.
Это то решение, которого мы хотели добиться, величина остаточных аберраций меньше одной двадцатой длины волны!
Теперь можем ввести углы поля зрения и провести тонкую доводку схемы. Из главного меню выберем System, Fields и доведем число направлений в поле зрения до трех. Введем Y- углы 0.0, 0.3 и 0.5 градусов. Если теперь обновите и посмотрите на график OPD, увидите, что для максимального поля величина комы составляет примерно 1/2 длины волны. Можем это
просто исправить, снова проведя оптимизацию. Так как мы ввели изменения в данные о поле зрения, то должны реконструировать нашу оценочную функцию! Это очень важно! Должны хорошо запомнить, что по умолчанию ZEMAX создает оценочную функцию на основе установленных направлений в поле зрения и длин волн; если изменили эти значения, Вы должны реконструировать оценочную функцию!
В окне редактора оценочной функции выберите Tools. Default Merit Function (при этом ZEMAX автоматически создаст новую оценочную функцию в соответствии с внесенными новыми данными о поле зрения и длинах волн) и измените число «Rings» на «4» . Нажмите на ОК. Теперь выберите из главного меню Tools, Optimization и нажмите на «Automatic».
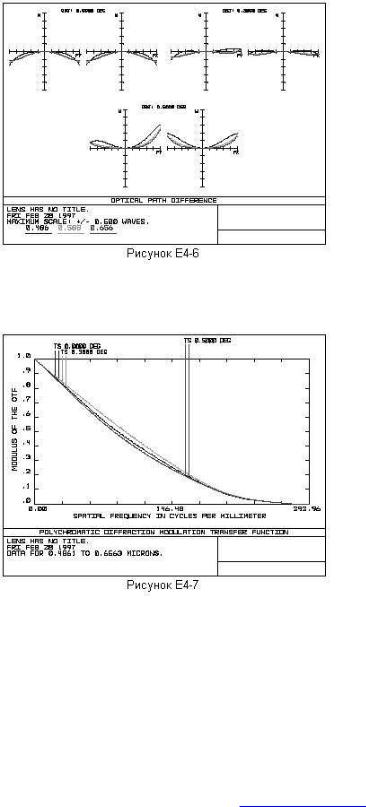
Когда процесс оптимизации закончится, нажмите на Exit и обновите еще раз график OPD. Полученный график показан на рис. Е4-6; он свидетельствует о хорошо сбалансированной схеме.
|
Предположим, |
что |
хотим |
||
|
использовать этот телескоп для получения |
||||
|
фотографий. Тогда нас может интересовать |
||||
|
модуляционная передаточная функция МПФ |
||||
|
(Modulation Transfer Function, MTF), которая |
||||
|
определяет |
контраст |
изображения |
в |
|
|
зависимости |
от пространственной |
частоты |
||
|
(измеряемой обычно в обратных милли— |
||||
|
метрах). Чтобы вывести на экран график |
||||
|
MTF. выберите из главного меню Analysis. |
||||
|
Diffraction. |
Modulation |
Transfer |
Function |
|
|
Появится график MTF вида, показанного на |
||||
|
рис. Е4-7 |
||||
|
График MTF является очень мощным |
||||
|
средством анализа качества оптической схемы. График показывает |
ход кривых |
MTF |
в |
меридиональной и сагиттальной плоскостях для всех определенных Вами направлений в поле зрения.
В этом графике, однако, имеется
|
некоторая |
погрешность. |
Опытный |
|
|
проектировщик |
заметит что |
полученный |
|
|
график |
представляет |
собой |
|
|
автокорреляционную |
функцию |
круглого |
|
|
зрачка. Дело в том, что |
не приняли в расчет |
имеющиеся в системе диафрагмы и экраны. В системе имеет место экранирование пучка, обусловленное вторичным зеркалом, и имеется отверстие в главном зеркале. Если мы учтем эти эффекты, характеристики системы ухудшаться, особенно в области средних пространственных частот. Для исправления этого недостатка в анализе обратимся вновь к
редактору LDE и дважды нажмем на первую колонку поверхности 1. В открывшемся окне откроем список типов апертурных поверхностей и выберем «Circular Aperture» (круглая апертура). В графе «Min Radius» (минимальный радиус) напечатаем 1.7. Это будет означать, что через эту поверхность будут проходить только те лучи, которые удалены от оси более чем на 1,7 дюймов; это будет моделировать отверстие («hole») в главном зеркале. Изменим величину
«Max Radius» до 6.
Моделирование эффекта экранирования лучей вторичным зеркалом немного сложнее. С

оптической точки зрения экран должен быть расположен перед вторичным зеркалом. Однако так как ZEMAX трассирует лучи последовательно от одной поверхности к другой, мы должны расположить экран перед главным зеркалом. Вообще говоря, проще будет сделать это, чем объяснить, так что немного доверьтесь нам и попробуйте сделать следующее. Установите курсор в строку поверхности 3 и нажмите на клавишу Insert. Этим будет введена новая поверхность между корректором и главным зеркалом. Измените, величину толщины этой новой поверхности (которая теперь имеет номер 3) от 0 до 20. Переместитесь на одну строку выше и измените толщину поверхности 2 от 60 до 40. При этом полное расстояние от корректора до главного зеркала останется неизменным и равным 60, мы просто ввели промежуточную поверхность. Дважды нажмите на элемент первой колонки в строке этой новой поверхности 3 и установите для нее тип апертуры «Circular Obscuration» (круглый экран). Напечатайте величину максимального (не минимального) радиуса экрана 2.5 в графе «Max Radius» (максимальный радиус) и нажмите на ОК. Установите также величину полудиаметра поверхности 3 равной 2.5. Теперь обновите окно с изображением схемы. Если Вы все сделали правильно, то схема будет выглядеть так, как показано на рис. Е4-8. Небольшой промежуток между экраном и вторичным зеркалом является делом вкуса; просто это позволяет лучше видеть схему. Если Вы хотите, то можете поместить экран прямо в вершину вторичного зеркала.
Функция MTF теперь претерпела изменение, вызванное введением экранов (главным образом, экрана вторичного зеркала), обновите окно с графиком MTF и посмотрите на новую функцию; ее вид показан на рис. Е4-9.
2.Требования к содержанию отчета. Отчет должен содержать:
— цель работы, — расчеты и схемы , — выводы.
3.Контрольные вопросы
1 Как используются полиномиальные асферические поверхности.
2.Экранирование, апертуры статус параметров.
3.Провести оптимизацию. Изобразить схемы, графики модуляционной передаточной функции.

К ЛАБОРАТОРНОЙ РАБОТЕ №5
Изучаются: Расширитель лазерного пучка. Использование режима мультиконфигурации.
Этот пример предполагает, что уже достаточно хорошо освоили работу с ZEMAX и знаете, как проводить основную диагностику оптических схем, такую как графики лучевых аберраций и OPD.
Предположим, что мы хотим спроектировать расширитель лазерного пучка для Работы с лазерным излучением с длиной волны 1.053 нм. Входной диаметр равен 100 мм, а выходной диаметр равен 20 мм. Оба пучка, входной и выходной, коллимированы. Такую схему несложно спроектировать, если нет ограничений на полную длину системы. Однако, чтобы усложнить эту задачу, мы установим несколько ограничений.
1)можно использовать только две линзы;
2)схема должна быть галилеевского типа (без внутреннего фокуса);
3)расстояние между линзами должно быть не более 250 мм;
4)допускается использование только одной асферической поверхности;
5)система должна тестироваться на длине волны 0,6328 мкм.
Эта задача требует не только коррекции аберраций, но и проведения такой коррекции для двух длин волн. Однако система не будет использоваться для работы на двух длинах волн одновременно, и поэтому мы можем изменить ее конфигурацию на время тестирования. Для начала запустим ZEMAX. Введем несколько поверхностей и установим статус переменной величины на параметры линз так, как это показано в нижеследующей таблице. Обратите внимание на то, что в показанной на рисунке таблице справа от колонки «Glass» есть колонка с названием «Focal Length» (фокальное расстояние)
Эта колонка появится в Вашем редакторе LDE только после определения типа поверхности «Paraxial» вместо «Standard». Этим мы введем в нашу схему на место данной поверхности модель параксиальной линзы. На рисунке для большей ясности показаны не все колонки.
Заметьте, что использование модели параксиальной линзы позволяет нам сфокусировать коллимированный пучок. Установите толщину этой поверхности и ее фокальную длину равными 25.00. Установите также диаметр входного зрачка равным 100(Для установки этой величины выберем в главном меню команду System, а затем, в развернувшемся на экране подменю, команду General. На экране появится новое диалоговое окно под названием «General Data» . Нажмите мышкой на элемент под названием «Aper Value» и введите число 100.) и введите длину волны 1.053 (в верхней части главного окна, выберем опцию System , а затем в выпавшем подменю — опцию Wavelengths ). Пока не вводите какую—либо другую длину волны.
Величины толщин линз были установлены произвольно, но этого для наших целей достаточно. Толщина 250 мм обусловлена нашим требованием #3. Теперь выберем Editors. Merit Function. Таблицу Merit Function нужно очистить, так чтобы на ней осталась только одна
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Слайд 1
Слайд 2
Описание слайда:
Zemax — это пакет программ, позволяющий моделировать, анализировать и проектировать оптические системы. Редактор данных оптической системы ”Lens Data Editor” (LDE) является главной таблицей, в которую вводится большинство параметров ОС. ZEMAX позволяет моделировать многие типы оптических компонентов со сферическими и асферическими поверхностями, а также тороидальными, цилиндрическими поверхностями, дифракционные решетки, бинарную оптику, линзы Френеля, голографические поверхности.
Zemax — это пакет программ, позволяющий моделировать, анализировать и проектировать оптические системы. Редактор данных оптической системы ”Lens Data Editor” (LDE) является главной таблицей, в которую вводится большинство параметров ОС. ZEMAX позволяет моделировать многие типы оптических компонентов со сферическими и асферическими поверхностями, а также тороидальными, цилиндрическими поверхностями, дифракционные решетки, бинарную оптику, линзы Френеля, голографические поверхности.
Слайд 3
Описание слайда:
Выбрав ”Analysis”, Вы получите результат вычислений в виде текстового или графического окна аберраций, МПФ, ФРТ, диаграмму пятна рассеяния и многое другое. Этот модуль может быть использован для моделирования протяженных источников, анализа разрешающей способности системы, анализа искажений изображения, получения общего представления о виде изображаемого объекта, для вычисления эффективности передачи излучения от точечного или протяженного источника через волокно. Анализ может быть основан как на геометрическом расчете хода лучей, так и на дифракционном подходе.
Выбрав ”Analysis”, Вы получите результат вычислений в виде текстового или графического окна аберраций, МПФ, ФРТ, диаграмму пятна рассеяния и многое другое. Этот модуль может быть использован для моделирования протяженных источников, анализа разрешающей способности системы, анализа искажений изображения, получения общего представления о виде изображаемого объекта, для вычисления эффективности передачи излучения от точечного или протяженного источника через волокно. Анализ может быть основан как на геометрическом расчете хода лучей, так и на дифракционном подходе.
Слайд 4
Описание слайда:
Оптимизация ОС проводится с целью улучшения ее характеристик или ее модификации для удовлетворения заданным требованиям. Эта программа осуществляет поиск глобального оптимума, который соответствует наилучшему из всех возможных решений оптической схемы для заданной оценочной функции и заданных переменных параметров. Программа осуществляет автоматически повторяющийся (итерационный) процесс оптимизации ОС с многократным переходом через локальный минимум оценочной функции. (Тонкая оптимизация схемы вблизи локального минимума).
Оптимизация ОС проводится с целью улучшения ее характеристик или ее модификации для удовлетворения заданным требованиям. Эта программа осуществляет поиск глобального оптимума, который соответствует наилучшему из всех возможных решений оптической схемы для заданной оценочной функции и заданных переменных параметров. Программа осуществляет автоматически повторяющийся (итерационный) процесс оптимизации ОС с многократным переходом через локальный минимум оценочной функции. (Тонкая оптимизация схемы вблизи локального минимума).
Слайд 5
Описание слайда:
Главное окно имеет несколько меню. Заголовки меню следующие:
Главное окно имеет несколько меню. Заголовки меню следующие:
File: Используется для открытия, закрытия, записи и переименования (save as) файлов с данными оптических систем.
Editors: Используется для вызова различных редакционных окон. System: используется для определение общих свойств оптической системы.
Analysis: Группы подпрограмм для анализа оптических схем; эти подпрограммы не изменяют параметры схемы, а выполняют численные расчеты и строят графики по данным текущей схемы. Это включает построение оптических схем, диаграмм, выполнение дифракционных вычислений и многое другое.
Слайд 6
Описание слайда:
Tools: «Инструменты» — программы, которые позволяют производить изменения параметров схемы или производить какие-либо операции над схемой в целом. Это включает оптимизацию, расчет и анализ допусков, подгонку радиусов кривизны под пробные стекла и другие.
Tools: «Инструменты» — программы, которые позволяют производить изменения параметров схемы или производить какие-либо операции над схемой в целом. Это включает оптимизацию, расчет и анализ допусков, подгонку радиусов кривизны под пробные стекла и другие.
Reports: Используется для документирования оптических схем; это включает суммарные данные по оптической системе и данные по отдельным оптическим поверхностям.
Macros: Используется для редактирования и выполнения ZPL программ (ZPL макросов).
Слайд 7
Описание слайда:
Extensions: Обеспечивает доступ к ZEMAX Extensions, которые являются внешними компилированными программами, работающими вместе с ZEMAX.
Extensions: Обеспечивает доступ к ZEMAX Extensions, которые являются внешними компилированными программами, работающими вместе с ZEMAX.
Window: Позволяет выбрать из списка всех ранее открытых окон нужное окно и расположить его на экране перед другими окнами.
Help: Обеспечивает доступ к справочным материалам по использованию ZEMAX.
Слайд 8
Описание слайда:
Конструктивные данные задаются в таблице редактора данных ОС (LDE – Lens Data Editor):
Конструктивные данные задаются в таблице редактора данных ОС (LDE – Lens Data Editor):
Surf – поверхность; Radius – радиус; Thickness – толщины; Glass – стекло; Semi-Diameter – высота; OBJ – предмет; STO – диафрагма; IMA – изображение.
Слайд 9
Описание слайда:
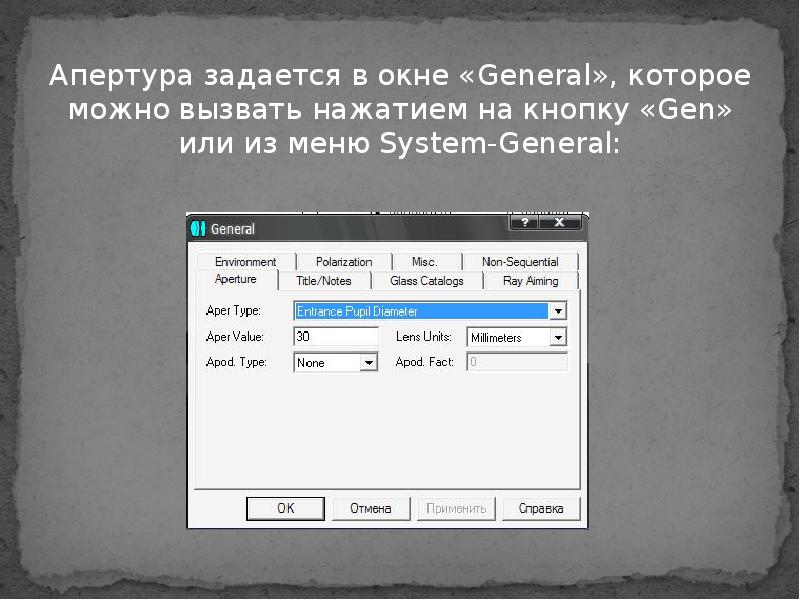
Апертура задается в окне «General», которое можно вызвать нажатием на кнопку «Gen» или из меню System-General:
Апертура задается в окне «General», которое можно вызвать нажатием на кнопку «Gen» или из меню System-General:
Слайд 10
Описание слайда:
Угловое поле 2ώ задается в окне Field Data, которое вызывается нажатием на кнопку «Fie» или из меню System-Fields:
Угловое поле 2ώ задается в окне Field Data, которое вызывается нажатием на кнопку «Fie» или из меню System-Fields:
Слайд 11
Описание слайда:
Спасибо за внимание
Спасибо за внимание
Время на прочтение
9 мин
Количество просмотров 56K
Построение идеальной оптики в Zemax
Введение
Всё больше современные системы автоматизации оснащаются оптическими устройствами для решения задач позиционирования, распознавания, наблюдения и др. Построение идеальных оптических систем при помощи программы расчета Zemax может оказаться полезным и непрофессионалам, например, для лучшего понимания теории, особенностей оптических устройств и выполнения прикидочных расчетов оптических систем. В этой работе рассмотрены приёмы построения идеальной оптики в среде Zemax, даны примеры расчета диапазона автофокусирования фотокамеры, построения эквивалентной схемы монокуляра МГТ 2.5×17.5, объектива фотокамеры SUNNY P13N05B смартфона Huawei P7 и замены идеальных оптических элементов реальными.
Идеальная оптика
Изображение в идеальной оптике, в которой отсутствуют искажения, строится по законам параксиальной оптики. Термин параксиальный означает «вблизи оси». Параксиальная оптика хорошо описываются линейными выражениями, которые при малых углах заменяются линейными уравнениями. В параксиальной области любая реальная система ведет себя как идеальная.
Расчеты идеальных линз в среде Zemax выполняются с допущением, что линзы имеют параксиальные свойства не только вблизи оси, но и на всей рабочей поверхности, которая действует как идеальная тонкая линза c единичным показателем преломления воздуха.
Параксиальную оптику целесообразно использовать в качестве эталона, с которым сравниваются аберрации (искажения) реальной оптики.
Переносить результаты расчетов параксиальной оптики на реальные системы следует с осторожностью, особенно при построении систем у которых свойства вблизи оптической оси и на удалении значительно отличаются.
Разработан целый ряд приёмов уменьшения аберраций и габаритных размеров линз: применение несферических поверхностей, составных линз, неоднородных оптических материалов, и др. Но как не была бы устроена реальная линза (Петцваля, Гаусса, Барлоу, …) ее характеристики могут только приближаться к характеристикам идеальной линзы.
Построение изображения собирающей линзой
Рассмотрим случай, когда от каждой точки плоскости предмета расходятся лучи во все стороны как от точечных источников. Из крайней точки объекта А, как показано на Рис. 1. в соответствующую точку В на плоскости изображения попадут только те лучи, которые сфокусированы линзой. Количество лучей предмета попадающих в плоскость изображения пропорционально диаметру линзы. Чем больше лучей от предмета попадает в плоскость изображения, тем выше яркость изображения.
Рис. 1. Сопряженные точки. Ход лучей от точки предмета к соответствующей точке
изображения на плоскости фотоприемника.
Для минимизации вычислений нахождения изображения рассматривают ход только нескольких лучей, например, как на Рис. 2: луч, идущий от объекта вдоль оптической оси; луч, проходящий через центр линзы и луч, параллельный оптической оси, преломляемый линзой и проходящий через главный фокус линзы (точка F на оптической оси).
Рис. 2. Минимальные построения для нахождения расстояния до плоскости изображения, величины изображения и увеличения линзы. Для параксиальной оптики продольное увеличение (связано с расстояниями) равно квадрату линейного увеличения (перпендикулярно оси), а угловое увеличение обратно пропорционально линейному.
Связь расстояний до предмета и изображения. Глубина резкости
Построение зависимости между зоной фокусировки объектива и глубиной резкости в пространстве предметов [1] показано на Рис. 3. Когда расстояние до предмета равно бесконечности, плоскость сфокусированного изображения проходит через главный фокус (смещение плоскости изображения относительно фокуса равно нулю). Минимальная глубина резкости в пространстве предметов достигается при максимальном удалении плоскости изображения (в зоне фокусировки) относительно главного фокуса.
Рис. 3. Зависимость между зоной фокусировки объектива и глубиной резкости в пространстве предметов.
Функции среды проектирования Zemax
Функции среды Zemax, наиболее часто используемые при проектировании оптических систем, присвоены отдельным кнопкам основного меню. Назначение этих кнопок показано на Рис. 4.
Рис. 4. Интерфейс программы Zemax.
Типы поверхностей элементов оптических систем, радиусы поверхностей, расстояния между элементами и другие параметры заносятся в таблицу редактора, в которой каждая строка содержит параметры одного элемента. Связь параметров таблицы и элементов оптической схемы показана на примере Рис. 5.
Рис. 5. Связь оптической схемы с параметрами таблицы.
Идеальная линза в Zemax
Для моделирования линзы с параксиальной поверхностью в Zemax необходимо задать фокусное расстояние и, при необходимости, включить расчет разницы оптических траекторий проходящих через линзу (установить статус OPD режима в 1 в соответствующей строке таблицы редактора). По умолчанию, OPD расчет не выполняется (статус OPD равен нулю [2]).
Построим в Zemax идеальную линзу, например, с диаметром входного зрачка 10 мм и фокусным расстоянием 15 мм, собирающую параллельные лучи удаленного предмета в одной точке.
1. Откроем новую таблицу: меню > кнопка
Рис. 6. Начальное состояние таблицы оптической схемы редактора Zemax. В строках таблицы (NN 0; 1 и 2) содержатся параметры предмета OBJ, апертурной диафрагмы STO и изображения IMA.
2. Добавим поверхность между диафрагмой и изображением: выделим последнюю строку строку IMA > меню Lens Data Editor > Edit > Insert Surface
Рис. 7. Добавлена стандартная поверхность N2.
3. Выберем «Параксиальный» тип поверхности: строка N2 > колонка Surf:Type > окно свойства — Properties > Surface Type > Paraxial
Рис. 8. Поверхность N2 изменена на идеальную (Paraxial) линзу с фокусным расстоянием 100 мм. Расстояние между линзой и изображением равно нулю. Расстояние между линзой и диафрагмой STO также равно нулю.
4. Изменим фокусное расстояние со 100 (по умолчанию) на 15 мм в колонке таблицы Focal Length
5. Зададим расстояние 15 мм от линзы до изображения в колонке Thickness
Рис. 9. Фокусное расстояние линзы изменено на 15 мм. Расстояние между линзой и изображением увеличено до 15 мм.
6. Зададим диаметр входного зрачка 10 мм: Основное меню > кнопка > закладка Aperture > Aperture Value > 10
Рис. 10. Задан диаметр входной апертуры оптической схемы: 10 мм.
7. Построим оптическую схему: Основное меню > кнопка
Рис. 11. Оптическая схема в окне Layout. Координаты диафрагмы и линзы совпадают (расстояние между ними равно нулю) Координаты “мышки” на схеме (в масштабе оптической схемы) отображаются в заголовке рисунка.
8. На схеме Layout не показаны лучи слева от идеальной линзы (выделена красным), идущие от предмета расположенного на бесконечном расстоянии, которое обозначено как Infinity в колонке Thickness нулевой строки OBJ таблицы. Чтобы показать часть этих лучей на входе линзы введем поверхность на расстоянии, например, 7 мм перед апертурной диафрагмой STO.
Рис. 12. Добавлена поверхность перед апертурной диафрагмой STO.
9. Добавим поверхность 1 к отображаемой части оптической схемы и увеличим количество лучей до 7 для наглядности: меню рисунка Layout > Setting > First Surface = 1 > Number of Rays = 7.
Рис. 13. Показаны лучи на отрезке 7мм до диафрагмы. Увеличено количество лучей с 3-х до 7.
10. Сделаем невидимой первую поверхность: строка N1 таблицы > колонка Surf:Type > окно свойства — Properties > закладка Draw >
11. Обновим окно Layout оптической схемы через кнопку основного меню или дважды «кликнув» в зоне окна схемы.
Рис. 14. Первая поверхность оптической схемы сделана невидимой.
В окне Layout можно отслеживать изменения табличных параметров оптической системы и параметров основного меню, показанных на Рис. 4 и Рис. 5.
Модель составной линзы фотокамеры смартфона
Для построения идеальной модели возьмем составную линзу фотокамеры SUNNY P13N05B смартфона Huawei P7 (Рис. 15). Линза смартфона состоит из пяти пластиковых элементов. Пример составной линзы показан на Рис. 16.
Рис. 15. Размеры [3] и фотографии фотокамеры SUNNY P13N05B с фотодиодной матрицей SONY IMX214 13 МП. 1. – модуль фотокамеры с фотодиодной матрицей; 2- линза камеры; 3 – катушка привода автофокусировки — перемещения объектива относительно матрицы датчика.
Камера P13N05B имеет следующие характеристики.
• Размер линзы: 1/3”
• Размер фотодиодной матрицы: 6,1 мм (H) × 4,5 мм (V)
• Диагональ активной зоны матрицы: 5,9 мм
• Состав линзы: 5 пластиковых элементов (см. Рис. 16)
• Фокусное расстояние: 3,79 мм
• Апертурное число (f/#): 2
• Угол поля зрения: 75°±3°
• Глубина резкости: от 7 см до ∞
• Диапазон привода автофокусировки: ≥ 0,24mm
Рис. 16. Пример составной линзы. Линза смартфона iPhone 6.
Параметры оптической схемы идеального объектива фотокамеры (см. Рис. 17) заданы в таблице Lens Data Editor и в окнах клавиш основного меню Zemax:. Функция выбираемая из списка функций выделенной ячейки колонки Thickness таблицы автоматически устанавливает наилучшее расстояние между линзой и изображением. Для построения наилучшего изображения удаленного на бесконечное расстояние предмета плоскость фотоприёмника должна проходить через точку главного фокуса отстоящей от линзы на 3,79 мм.
Рис. 17. Оптическая схема параксиальной линзы фотообъектива. Предмет удален на бесконечное расстояние.
Приближение объекта к линзе на 10 мм с сохранением угла обзора 76о/2 в окне Field Data (Рис. 18) увеличило расстояние между линзой и изображением до 6,10 мм. Следовательно изменение автофокуса при приближении объекта с бесконечности до 10 мм равно 2,31 мм (как 6,10 мм – 3,79 мм).
Рис. 18. Построение лучей от объекта находящегося в 10 мм от параксиальной линзы фотокамеры и нахождение положения автофокуса.
В спецификации фотокамеры P13N05B указано, что глубина резкости в пространстве предметов лежит в пределах от 7 см до ∞ (бесконечности). Установим предмет на минимальной дистанции в 70 мм от апертурой линзы. Zemax устанавливает расстояние между линзой и плоскостью изображения 4 мм (см. выделенную ячейку таблицы на Рис. 19). Таким образом, для построения качественного изображения предмета находящегося в зоне от 7 см до ∞ требуется изменять расстояние между линзой и фотодатчиком от 4 до 3,79 мм. Требуемое изменение 0,21мм перекрывается диапазоном привода автофокусировки фотокамеры 0,24 мм.
Рис. 19. Расстояние до изображения равно 4 мм при расстоянии до объекта 70 мм. Фокусное расстояние линзы равно 3,79 мм.
Зависимость диапазона фокусировки от фокусного расстояния объектива
Зона фокусировки зависит не только от дистанции до предмета, но и от главного фокуса линзы (объектива). На Рис. 20 показана геометрия нахождения зон фокусировки для линз с главным фокусом F1=7,5 мм и F2=19 мм и положений предмета в диапазоне AB = 35… 52 мм. Для настройки резкости с линзой F1 требуется изменять расстояние меду главным фокусом линзы и плоскостью изображения в диапазоне 0,8 мм, тогда как для линзы с F2 этот диапазон вырос до 12 мм.
Рис. 20. Пример построения зон фокусировки для линз с разными фокусными расстояниями F1 и F2.
Идеальные телескопы
Сравнительные размеры телескопов Кеплера и Галилея для одинакового увеличения F1/F2 показаны на Рис. 21. Телескоп Кеплера с собирающими линзами даёт перевернутое изображение. Более компактный телескоп Галилея включает рассеивающую линзу и даёт прямое изображение.
Рис. 21. Схема телескопов Кеплера (а) и Галилея (б) при одинаковом увеличении F2/F1.
Миниатюрный монокуляр МГТ 2,5×17,5 СССР, ЛЗОС (Лыткаринский завод оптического стекла) собран по схеме Галилея (Рис. 22). Он имеет следующие характеристики.
• Увеличение: 2,5 крат(раз)
• Диаметр объектива: 17,5 мм
• Угол поля зрения: 13,5 град
• Разрешающая способность: 15 угл. сек
• Предел фокусировки окуляра: -5…+5 диоптр
• Габаритные размеры: 22 x 38 мм
Рис. 22. Вид и примерные размеры миниатюрного монокуляра МГТ 2,5×17,5. Предмет находится справа.
Эквивалентная идеальная оптическая схема монокуляра МГТ 2,5×17,5 в ZEMAX показана на Рис. 23. Схема состоит из собирающей и рассеивающей линз с главными фокусами 37,5 мм и -15 мм соответственно, имеющими отношение 2,5 раз. Диаметр собирающей линзы 2х8,75 мм.
Рис. 23. Табличные данные и идеальная оптическая схема монокуляра МГТ 2,5×17,5. Параллельные лучи идут от предмета удаленного на бесконечное расстояние.
Вариант замены параксиальной линзы реальной
Заменим первую параксиальную линзу (диаметр: 17,5 мм; фокусное расстояние: 37,5 мм) монокуляра ахроматической линзой из каталога Edmund Optics [4]. Чтобы минимизировать выборку линз установим следующие условия: категория — Achromatic Lenses; диаметр – 18 мм; эффективная фокальная длина EFL 30-39.99 мм; диапазон длин волн — 425 — 675 нм.
Ближайшая к требуемым параметрам линза: 18mm Dia. x 35mm FL, VIS 0° Coated, Achromatic Lens, Stock No. #47-706 (номер по каталогу).
Для построения ахроматической линзы в Zemax из ее спецификации возьмем параметры перечисленные в Таблица 1. Параметры можно найти и на чертеже линзы PDF drawing сайта Edmund Optics [4] или на Рис. 24.
Таблица 1. Параметры составной ахроматической линзы Edmund #47-706
| Параметр | Значение | Примечание |
|---|---|---|
| Diameter | 18,0 мм | Диаметр |
| Clear Aperture CA | 17,0 мм | Диафрагма |
| Effective Focal Length | 35,0 мм | Эффективное фокусное расстояние |
| Center Thickness CT 1 | 6,01 мм | Толщина 1-го элемента по оси |
| Center Thickness CT2 | 1,60 мм | Толщина 2-го элемента по оси |
| Radius R1 (mm) | 24,26 мм | Радиус первой поверхности |
| Radius R2 (mm) | 16,23 мм | Радиус второй поверхности |
| Radius R3 (mm) | -152,99 мм | Радиус третьей поверхности |
| Substrate | N-BAF10 / N-SF10 | Материалы элементов |
Рис. 24. Чертеж ахроматической линзы Edmund #47-706.
Замена параметров первой линзы идеального телескопа (строка N2 таблицы Рис. 23) линзой Edmund #47-706 даёт вариант, представленный на Рис. 25.
Рис. 25. Вариант оптики телескопа с реальной ахроматической линзой. Выделенное в таблице красным расстояние между линзами найдено ручным смещением движка Slider.
Расстояние между линзами (выделенное красным в таблице Рис. 25) изменялось ползунком Slider в ручную до момента когда лучи на выходе второй (идеальной линзы) установились параллельными главной оси (в этом положении фокусные расстояния линз телескопа находятся в одной точке). Действие ползунка в реальном времени отображается смещением элементов оптической схемы и изменением траекторий лучей на оптической диаграмме окна Layout. Ползунок можно открыть через основное меню Zemax > Tools > Miscellaneous > Slider.
Если на выходе телескопа поставить дополнительную параксиальную собирающую линзу (элемент N6 в таблице и красная плоскость на оптической схеме Рис. 26), то можно увидеть вносимые реальной линзой искажения (см. часть диаграмм Zemax на Рис. 26).
Рис. 26. Оптическая схема и диаграммы искажений, вносимые реальной линзой.
Литература
1. Сайт Optics Realm. Видеоуроки по проектированию в среде Zemax и теории оптики. www.opticsrealm.com
2. Zemax Help > Optical Design Program User’s Guide .pdf
3. H&L ELECTRICAL MANUFACTORY LIMITED hnl.en.e-cantonfair.com/products/sunny-brand-p13n05b-imx214-sony-sensor-13-0m-pixel-mipi-csi-1080p-sunny-cmos-camera-module-552104.html
4. Edmund Optics. www.edmundoptics.com/optics/optical-lenses
5. Dr. Bob Davidov. Компьютерные технологии управления в технических системах portalnp.ru/author/bobdavidov.
← Вернуться в раздел «Программы»
Подскажите где можно взять описание всех операндов оптимизации для Zemax 2009? И где можно найти полную инстукцию на русском языке?
Автор: DSER
Дата сообщения: 13.05.2011 08:31
BernikG
На книголюб ушли
…
580 ZEMAX: Руководство пользователя (2010)
Автор: BernikG
Дата сообщения: 13.05.2011 08:33
DSER
как туда попасть?
Автор: DSER
Дата сообщения: 13.05.2011 08:36
#
Автор: BernikG
Дата сообщения: 13.05.2011 08:51
DSER
А сылка есть? че то я туплю и не могу понять или найти!
Автор: A_P_V
Дата сообщения: 13.05.2011 08:58
BernikG
щелкни на «редактировать» в сообщении DSERa c #.
Автор: BernikG
Дата сообщения: 13.05.2011 09:01
A_P_V
Блаходарю!
Автор: asorokovik
Дата сообщения: 13.05.2011 13:16
Здравствуйте.
Кто делал UserDefinedObject с помощью DLL в C++? Проблема в передаче данных из DLL в NSC Editor, т.е. функция пересчитывает параметры, ограничения и хотелось бы отобразить изменения в NSCEditore для дальнейшей передаче оптимизатору.
Очень хорошо это реализовано у объекта Array (после установки параметров видны геометрические размеры фигуры — readonly)
Спасибо
Автор: ging
Дата сообщения: 13.05.2011 14:40
Цитата:
хотелось бы отобразить изменения в NSCEditore для дальнейшей передаче оптимизатору
Это невозможно, обмен идет только в одну сторону: из Editor’а в ДЛЛ.
Автор: linkoff
Дата сообщения: 13.05.2011 19:01
Цитата:
Ладно, я понимаю что у вас лобби Lighttools на фирме слишком сильное.
Да нет, я считаю и в Zemax и в Lighttools. ЧТо то там, что то там. Есть народ который в ASAP считает.
Автор: Blaze63rus
Дата сообщения: 14.05.2011 00:00
Цитата:
Цитата: Так сказать, я просто не знаю как правильно задать вопрос.
А как вы задаёте источник света (в Трэйсе)?
Ведь фара это источник + отражатель/рассеиватель.
У меня в сборе:
1. лампа
2. отражатель
3. светорассеиватель
лампа состоит из колбы и спирали, представленной в виде цилиндра. Цилиндр образован 2мя боковыми плоскостями и торцевыми. Так вот я задаю на эти 2 плоскости цилиндра источники света в 460 люмен каждый (лампа 460 люмен). Тип поверхности источника задал «нормальная поверхность».
Материал колбы лампы, светорассеивателя и отражателя тоже заданы, зеркальная поверхность отражателя задана.
Автор: yevogre
Дата сообщения: 14.05.2011 09:10
Цитата:
Тип поверхности источника задал «нормальная поверхность».
А почему нормальная? Там надобен Ламберт ИМХО.
Нормаль даёт очень большую ошибку, я один раз сдуру использовал — меня заказчик после прототипирования чуть не съел.
Благо дело далеко он от меня.
Автор: linkoff
Дата сообщения: 14.05.2011 13:02
Цитата:
просто пример: до 100 длин волн (Manual 2009.06, стр 414 ).
Так что при желании все возможно. А кстати, каждая копия Lighttools так и считает в одном потоке? Тогда никакого выигрыша по сравнению с Зем: те же вычисления запускаются последовательно макросом из нескольких строк.
Ну кстати не знал, раньше было 20. Каждая копия LT считает в одном потоке, и это не удобно.
Автор: DSER
Дата сообщения: 14.05.2011 14:10
Мелочь, а приятно…
Не зря создавалась тема, т.к. востребована.
Судя по первому сообщению тема появилась 21-01-2005, уже 6 лет…

Только сейчас я об этом задумался.
Автор: A_P_V
Дата сообщения: 14.05.2011 19:49
Да, тема ценная. Аналогичных русскоязычных форумов больше не знаю. http://physics-animations.com/cgi-bin/forum.pl?forum=opt — здесь очень редко что появляется.
Автор: basilio_ef
Дата сообщения: 15.05.2011 14:20
DSER
Цитата:
На книголюб ушли
…
580 ZEMAX: Руководство пользователя (2010)
В моем посте от 30.04.2011 (стр. 14) дана ссылка на это же руководство(ZEMAX-Optical_Design_Program.Users_Manual), но с ПОЛНЫМ BOOKMARKS.
Автор: BeA1ive
Дата сообщения: 16.05.2011 11:21
Всем здравствуйте, я вернулся. 
Есть вопрос — как в Zemax задать условие волновой аберрации в волнах (например, 0,1 длины волны).
Пробовал OPDM — задавал координаты и target 0,1 (например), но качество только падало. Радиуса, толщины, расстояния — всё Variable.
Автор: mp2004
Дата сообщения: 17.05.2011 11:04
BeA1ive
Я бы использовал RWCH без веса, а в следующей строке OPLT. Вот только зачем? По умолчанию все «стремится» к 0.
Автор: BeA1ive
Дата сообщения: 19.05.2011 20:07
Цитата:
Я бы использовал RWCH без веса, а в следующей строке OPLT. Вот только зачем? По умолчанию все «стремится» к 0.
Дельный совет! Помогло!
Попробовал RWCH + OPLT — лямбда/30 стало (было лямбда/10).
Потом попробовал только RWCH — тоже получилось. Но тут чем больше вес (10) и Ring (10 поставил), тем лучше. Только не понял с target — аж 0.0001 пришлось ввести, хотя, по идее, и 0,05 должно хватить было, но тогда лямбда/15 только.
P.S.: Убрал OPLT, поставил в RWCH вес=1000, target=0,0000001, ring=20 получил лямбда/88 у упёрся, но больше и не надо. Вес решает!
Автор: A_P_V
Дата сообщения: 20.05.2011 10:09
BeA1ive
в простых системах может и решает, но в сложных зачастую приходится веса подбирать в диалоговом режиме.
Автор: Blaze63rus
Дата сообщения: 20.05.2011 23:18
Цитата:
[/q][q]А почему нормальная? Там надобен Ламберт ИМХО.
Нормаль даёт очень большую ошибку, я один раз сдуру использовал — меня заказчик после прототипирования чуть не съел.
Благо дело далеко он от меня.
Да сделал уже сразу стало близко к истине. Картинка очень похожа на оригинал. Вот только значения в 3 раза больше чем у оригинала.
И еще можно как-нибудь вывести таблицу значений в указанных точках, а то я что-то не нашел.
(Прог. Trace Pro)
Автор: Blaze63rus
Дата сообщения: 23.05.2011 13:19
и еще как задать (расчитать) коэф. поглощения материала. Материал у меня полиметилметакрилат. у него светопропускание 90%
Автор: paparazzo
Дата сообщения: 23.05.2011 13:54
Цитата:
и еще как задать (расчитать) коэф. поглощения материала. Материал у меня полиметилметакрилат. у него светопропускание 90%
Такой нюанс. 
Что есть светопропускание и чем оно обусловлено?
Есть внутренее светоппропускание материала. У пмма оно далеко не 90%, а зависит еще от толщины слоя, т.е. от пути луча. Закон Бугера. Также существует зависимость коэффициента поглощения от интенсивности света, видел даже статью на эту тему где-то..
А 90% Обусловлено большей частью френелевским отражением света на границе раздела. Причем интенсивность отраженного света зависит от угла падения луча.
Т.е. задавать 90% — неправльно.
А задается оно в редакторе каталога стекол Zemax, в виде таблицы. Внутреннее пропускание пмма где-то >99% в области 400-700 нм для толщины слоя в дюйм.
Добавлено:
А Френелевское отражение Zemax учтет автоматиечески при включенной опции «Split Rays»
Автор: Blaze63rus
Дата сообщения: 24.05.2011 07:45
спасибо за ответ. но я работаю с TracePro. Хотелось бы услышать ответ на мой вопрос относительно этой программы.
Там есть пункт для материала absorption (/мм), и я не совсем понимаю что именно подразумевается под этим коэф. и в какой размерности его задавать
Автор: paparazzo
Дата сообщения: 24.05.2011 10:25
Цитата:
спасибо за ответ. но я работаю с TracePro. Хотелось бы услышать ответ на мой вопрос относительно этой программы.
Там есть пункт для материала absorption (/мм), и я не совсем понимаю что именно подразумевается под этим коэф. и в какой размерности его задавать
В TracePro опция SplitRays всегда «включена», т.е. он трассирует лучи с учетом Френелевского отражения, если не заданы покрытия.
absorption — это коэффициент из закона Бугера (Beer’s law), о котором я писал выше. I=I0*exp(-a*L), ‘I’ — интенсивность вышедшего из среды света, ‘I0’ — начальная интенсивность, ‘a’ — ваш коэффициент, ‘L’ — путь луча света в среде в миллиметрах, если ‘а’ в 1/mm.
Добавлено:
Ставьте absorption=0, если у вас конечно не метровые толщины оптики.
Автор: Blaze63rus
Дата сообщения: 24.05.2011 13:10
при absorption =0 результаты расчетов отличаются от настоящих в 3 раза в большую сторону.
у меня рассеиватель 3мм толщиной. сейчас я просто поигравшись с этим коэф. добился сооответствия значения. коэф. у меня получился 0.6
Но здесь я знаю какая цифра должна получиться, но вторым этапом мне надо будет рассчитать значения не имея готового фонаря. т.е. мне надо знать точно все коэф-ты и как их вводить
Автор: paparazzo
Дата сообщения: 24.05.2011 14:37
Цитата:
у меня рассеиватель 3мм толщиной.
Так у вас рассеиватель, а не прозрачный пластик?
Коэффициент этот порядка 0.0005, но никак не 0.6….
И вопрос — что есть настоящие значения? Например самая трудноинтерпретируемая величина — яркость, куча методов измерения и моделирования…. В стандарте соответствующем описывается методика измерения. И часто не все друг-друга понимают.
Хотя она и самая важная в таких задачах.
Другое дело — сила света или освещенность, там все понятно.
А можно схему фары, или даже лучше файл TracPro?
Автор: Blaze63rus
Дата сообщения: 24.05.2011 16:25
рассеиватель — это прозрачный пластик с некоторой рельефной поверхностью с внутренней стороны
Нас интересует непосредственно сила света и освещенность.
Вот сила света (кд) и расходиться с реально измеренным значением (т.е. измеренным прибором)
Автор: A_P_V
Дата сообщения: 24.05.2011 16:41
У вас есть возможность промерить без рассеивателя? Тогда можно убедиться, что источник + отражатель промоделированы правильно.
Автор: Blaze63rus
Дата сообщения: 24.05.2011 17:03
нет, такой возможности нет. т.к. блок фары склеен
Страницы: 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378
Предыдущая тема: Maxthon 3.x — быстрый и мощный браузер
Форум Ru-Board.club — поднят 15-09-2016 числа. Цель — сохранить наследие старого Ru-Board, истории становления российского интернета. Сделано для людей.
Слайд 1
Слайд 2
Описание слайда:
Zemax — это пакет программ, позволяющий моделировать, анализировать и проектировать оптические системы. Редактор данных оптической системы ”Lens Data Editor” (LDE) является главной таблицей, в которую вводится большинство параметров ОС. ZEMAX позволяет моделировать многие типы оптических компонентов со сферическими и асферическими поверхностями, а также тороидальными, цилиндрическими поверхностями, дифракционные решетки, бинарную оптику, линзы Френеля, голографические поверхности.
Zemax — это пакет программ, позволяющий моделировать, анализировать и проектировать оптические системы. Редактор данных оптической системы ”Lens Data Editor” (LDE) является главной таблицей, в которую вводится большинство параметров ОС. ZEMAX позволяет моделировать многие типы оптических компонентов со сферическими и асферическими поверхностями, а также тороидальными, цилиндрическими поверхностями, дифракционные решетки, бинарную оптику, линзы Френеля, голографические поверхности.
Слайд 3
Описание слайда:
Выбрав ”Analysis”, Вы получите результат вычислений в виде текстового или графического окна аберраций, МПФ, ФРТ, диаграмму пятна рассеяния и многое другое. Этот модуль может быть использован для моделирования протяженных источников, анализа разрешающей способности системы, анализа искажений изображения, получения общего представления о виде изображаемого объекта, для вычисления эффективности передачи излучения от точечного или протяженного источника через волокно. Анализ может быть основан как на геометрическом расчете хода лучей, так и на дифракционном подходе.
Выбрав ”Analysis”, Вы получите результат вычислений в виде текстового или графического окна аберраций, МПФ, ФРТ, диаграмму пятна рассеяния и многое другое. Этот модуль может быть использован для моделирования протяженных источников, анализа разрешающей способности системы, анализа искажений изображения, получения общего представления о виде изображаемого объекта, для вычисления эффективности передачи излучения от точечного или протяженного источника через волокно. Анализ может быть основан как на геометрическом расчете хода лучей, так и на дифракционном подходе.
Слайд 4
Описание слайда:
Оптимизация ОС проводится с целью улучшения ее характеристик или ее модификации для удовлетворения заданным требованиям. Эта программа осуществляет поиск глобального оптимума, который соответствует наилучшему из всех возможных решений оптической схемы для заданной оценочной функции и заданных переменных параметров. Программа осуществляет автоматически повторяющийся (итерационный) процесс оптимизации ОС с многократным переходом через локальный минимум оценочной функции. (Тонкая оптимизация схемы вблизи локального минимума).
Оптимизация ОС проводится с целью улучшения ее характеристик или ее модификации для удовлетворения заданным требованиям. Эта программа осуществляет поиск глобального оптимума, который соответствует наилучшему из всех возможных решений оптической схемы для заданной оценочной функции и заданных переменных параметров. Программа осуществляет автоматически повторяющийся (итерационный) процесс оптимизации ОС с многократным переходом через локальный минимум оценочной функции. (Тонкая оптимизация схемы вблизи локального минимума).
Слайд 5
Описание слайда:
Главное окно имеет несколько меню. Заголовки меню следующие:
Главное окно имеет несколько меню. Заголовки меню следующие:
File: Используется для открытия, закрытия, записи и переименования (save as) файлов с данными оптических систем.
Editors: Используется для вызова различных редакционных окон. System: используется для определение общих свойств оптической системы.
Analysis: Группы подпрограмм для анализа оптических схем; эти подпрограммы не изменяют параметры схемы, а выполняют численные расчеты и строят графики по данным текущей схемы. Это включает построение оптических схем, диаграмм, выполнение дифракционных вычислений и многое другое.
Слайд 6
Описание слайда:
Tools: «Инструменты» — программы, которые позволяют производить изменения параметров схемы или производить какие-либо операции над схемой в целом. Это включает оптимизацию, расчет и анализ допусков, подгонку радиусов кривизны под пробные стекла и другие.
Tools: «Инструменты» — программы, которые позволяют производить изменения параметров схемы или производить какие-либо операции над схемой в целом. Это включает оптимизацию, расчет и анализ допусков, подгонку радиусов кривизны под пробные стекла и другие.
Reports: Используется для документирования оптических схем; это включает суммарные данные по оптической системе и данные по отдельным оптическим поверхностям.
Macros: Используется для редактирования и выполнения ZPL программ (ZPL макросов).
Слайд 7
Описание слайда:
Extensions: Обеспечивает доступ к ZEMAX Extensions, которые являются внешними компилированными программами, работающими вместе с ZEMAX.
Extensions: Обеспечивает доступ к ZEMAX Extensions, которые являются внешними компилированными программами, работающими вместе с ZEMAX.
Window: Позволяет выбрать из списка всех ранее открытых окон нужное окно и расположить его на экране перед другими окнами.
Help: Обеспечивает доступ к справочным материалам по использованию ZEMAX.
Слайд 8
Описание слайда:
Конструктивные данные задаются в таблице редактора данных ОС (LDE – Lens Data Editor):
Конструктивные данные задаются в таблице редактора данных ОС (LDE – Lens Data Editor):
Surf – поверхность; Radius – радиус; Thickness – толщины; Glass – стекло; Semi-Diameter – высота; OBJ – предмет; STO – диафрагма; IMA – изображение.
Слайд 9
Описание слайда:
Апертура задается в окне «General», которое можно вызвать нажатием на кнопку «Gen» или из меню System-General:
Апертура задается в окне «General», которое можно вызвать нажатием на кнопку «Gen» или из меню System-General:
Слайд 10
Описание слайда:
Угловое поле 2ώ задается в окне Field Data, которое вызывается нажатием на кнопку «Fie» или из меню System-Fields:
Угловое поле 2ώ задается в окне Field Data, которое вызывается нажатием на кнопку «Fie» или из меню System-Fields:
Слайд 11
Описание слайда:
Спасибо за внимание
Спасибо за внимание